안녕하세요. 푸디헬스입니다.
2017년 9월 6일 수요일 평가원이 주관한 대학수학능력시험 9월 모의평가 수학 가형 21번입니다. 이번 모의고사에서 오답률 60%로 3위를 차지했던 문제입니다.

발문을 처음부터 끝가지 차근차근 읽은 뒤에 문제를 발문 순서대로 풀어보겠습니다.
발문에서 가장 먼저 수열을 정의했습니다.
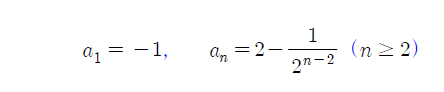
수열을 차례대로 써보면 $a_1 = -1, a_2 = 1, a_3 = 2-\frac12, a_4=2-\frac14$, $a_5=2-\frac18$로 됩니다. 그러고 나서 다음 발문을 보겠습니다.

$f(x)$를정의했고 $\alpha$의 구간이 주어진 다음 정적분에 대한 조건이 나왔습니다. 그럼 가장 먼저 $f(x)$를 정의했으므로 $f(x)$를 그려보겠습니다.
$n=1$일때, $f(x)=sin(2\pi x)(-1\le x \le1)$ 주기 1
$n=2$일때, $f(x)=sin(4\pi x)(1\le x \le 2-\frac12)$ 주기 $\frac12$
$n=3$일때, $f(x)=sin(8\pi x)(2-\frac12 \le x \le 2-\frac14)$ 주기 $\frac14$
$n=4$일때, $f(x)=sin(16\pi x)(2-\frac14 \le x \le 2-\frac18)$ 주기 $\frac18$
이므로 아래와 같이 나옵니다.

그러고 나서 다음 조건을 보겠습니다.

$\alpha$의 범위가 주어졌고 적분에 관한 식이 나왔습니다. 그럼 이것을 그림으로 표현해보겠습니다.
$\int_{\alpha}^{t} f(x) dx = 0$을 만족하는 $t$가 103개라고 하였습니다. 이 식을 이해하기 위해 작은 수부터 넣어보겠습니다. $\alpha$에서 $0$까지 $f(x)$의 넓이가 $\frac12$때 $t$의 개수를 살펴보겠습니다.
그전에 $sin$함수의 특징을 설명해드리면 $sin(x)$가 $asin(bx)$로되면 한 봉우리의 넓이는$\frac{a}{b}$가 됩니다.
즉 $sin(x)$의 한봉우리 넓이가 2라면 $2sin(2\pi x)$의 한 봉우리의 넓이는 $2 \times \frac{2}{2\pi}$가 됩니다.(실제 $sin(x)$의 한봉우리 넓이는 2입니다.)
다시 문제로 돌아와서 $\alpha$에서 $0$까지 $f(x)$의 넓이가 $\frac12$때 $t$의 개수를 살펴보겠습니다.($f(x)$에 $\pi$가 들어가서 넓이에 원래는 $\pi$가들어가지만 규칙만 찾기 위해 편하게 넓이를 $\frac12$라고했습니다.)

$\alpha$가 검은선부터 시작해서 $\int_{\alpha}^{t} f(x) dx = 0$를 만족하는 $t$(보라색선)는 총 3개가 나옵니다.
이해를 돕기 위해 $\alpha = 1/4$일때 한번 더 해보겠습니다.
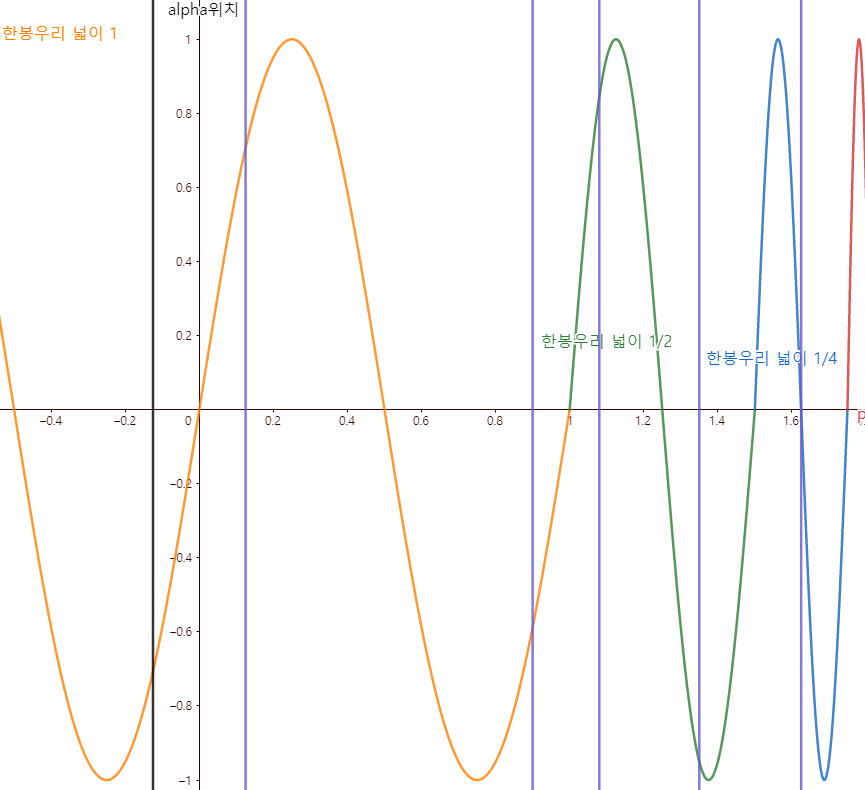
$\alpha$가 검은선부터 시작해서 $\int_{\alpha}^{t} f(x) dx = 0$를 만족하는 $t$(보라색선) 총 5개가 나옵니다.
마지막 파란봉우리가 끝나는 지점이 성립하는 이유는 $-\int_{\alpha}^{0} f(x) dx = \frac14$이 성립하는 $\alpha$값을 잡았기 때문입니다. 그럼 위의 2개를 예시로 저희는
$-\int_{\alpha}^{0} f(x) dx = \frac12$일때 $t$의 개수가 3개
$-\int_{\alpha}^{0} f(x) dx = \frac14$일때 $t$의 개수가 5개 인 것을 알 수 있습니다. 이것을 일반화해보면
$-\int_{\alpha}^{0} f(x) dx = 2^{-n}$일때 $t$의 개수는 $2n+1$가 됩니다.
발문에서 $\int_{\alpha}^{t} f(x) dx = 0$을 만족하는 $t$의 개수가 103개라고 하였으므로, $2n+1 = 103$을 풀면
$n=51$이 되고 $-\int_{\alpha}^{0} f(x) dx = \frac{2^{-51}}{\pi}$가 됩니다.(여기서부터는 넓이를 정확하게 쓰겠습니다. 그래서 넓이에 $\pi$를 넣었습니다.)
$\int_{\alpha}^{t} f(x) dx = 0$를 $-\int_{\alpha}^{0} f(x) dx = \int_{0}^{t} f(x) dx$변형하여 풀면
$\frac{1}{2 \pi}(1-cos(2 \pi \alpha)) = \frac{2^{-51}}{\pi}$
$1-cos(2 \pi \alpha) = 2^{-50}$이 됩니다.

그러므로 정답은 ②이됩니다. 발문 순서대로 풀면 이번 문제도 어렵지 않게 풀리는 문제였습니다.
2018 고3 9월모의고사 수학 가형 30번
모의고사 - 2018 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 가형 30번 풀이
안녕하세요. 푸디헬스입니다. 수학시험을 볼 때 가져야 할 태도는 어떤 게 있을까요? 여기서 태도라고 하는 것은 가장 좋은 점수를 받는 태도를 의미합니다. 수학시험에는 30문제를 푸는 데 100분이 주어집니다...
foodiehealth.tistory.com
2018 고3 9월모의고사 수학 가형 29번
모의고사 - 2018 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 가형 29번
안녕하세요. 푸디헬스입니다. 수학 공부를 하는데 어떻게 공부를 해야 좀 더 효율적으로 할 수 있는지 고민하시는 분들이 계실 겁니다.(어떻게 하면 적은 시간으로 빠르고 정확하게 문제를 풀 수 있을까?) 수학은..
foodiehealth.tistory.com
잘 이해가 가지 않거나 다른 문제의 풀이가 궁금하신 분은 댓글을 남겨주시기 바랍니다. 감사합니다.




댓글