2018수능수학가형 29,30번 짝수형 문제풀이(대학수학능력시험)

2018수능 수학 가형(짝수).pdf

0.54MB

2018수능 수학 가형(짝수)_답지.pdf

0.08MB

안녕하세요. 푸디헬스입니다.

2018 수능 수학 29번 오답률은 약 94%, 30번 오답률은 약 95%로 수험생들이 실전에서 어려워했던 문제입니다. 앞으로 얼마 남지 않은 수능 대비를 위해 전년도 수능 기출문제 분석은 필수입니다. 그럼 이문제를 실전에서 어떻게 접근하는지 같이 한번 풀어보겠습니다.

29번입니다.

발문에서 평면 $ x+2z-5=0 $라고 하였습니다. 여기서 문자 $y$가 없습니다. 그러므로 주어진 평면은 $y$축과 평행합니다.(이조건은 매우 중요합니다.) 그러므로 주어진 구와 평면을 3차원으로 나타내 보겠습니다. 

( x축 : 빨강, y축 : 초록, z축 : 파랑)

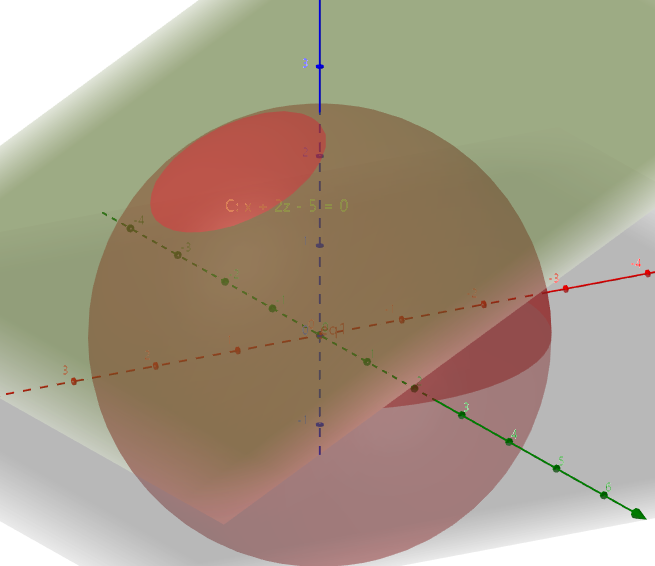
그럼 평면 $C$는 빨간색과 같이 나오게 됩니다.

그런데 원 $C$의 중심은 $xz$평면에서 원 $x^2+z^2=6$과 직선 $x+2z-5=0$이 만나는 점의 중점이므로

$x+2z-5=0$과 수직이고 원점을 지나는 직선$z=2x$와 직선$x+2z-5=0$과의 교점이 점 $C$의 중심이 됩니다.

 

x축, z축입니다. (x, z)

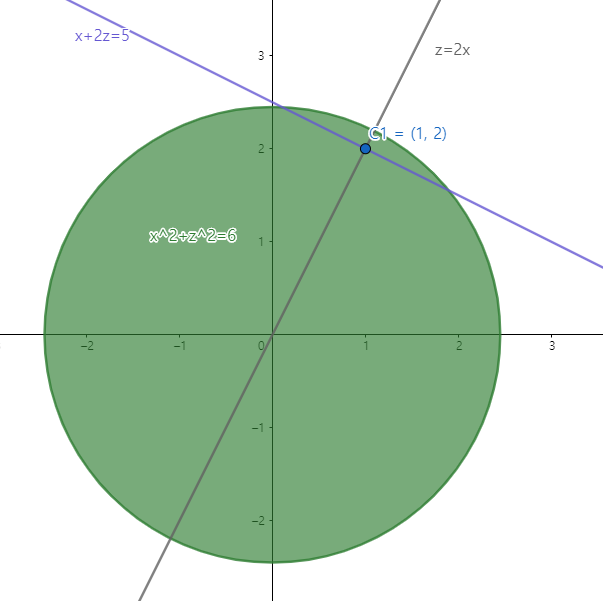
그래서 $z=2x$과 $x+2z-5=0$를 연립하면 원$C$의 중점은 (1, 0, 2)가 되고 원점과의 거리는 $\sqrt{5}$이고 구의 반지름은 1이므로 원 $C$ 의 반지름은 1이 됩니다. 

 

 

원 C위의 점 중 y좌표가 최소인 점을 P라고 하였으므로 원 $C$의 중점이 $(1, 0, 2)$이고 반지름이 1이므로 점 $P$는

$(1, -1, 2)$가되고, 점 $P$에서 $xy$평면에 내린 수선의 발을 $Q$라고 하였으므로 점 $Q$는 $(1, -1, 0)$이 됩니다.(주어진 평면이 y축과 평행하기 때문에 원 C가 y축과 평행합니다.)

그리고 발문에서 원 C 위를 움직이는 점 X라고 명시해놓았으므로 발문에서 시키는 대로 $X$를 $(x, y, z)$로 잡습니다.

점 X(x, y, z) P(1, -1, 2) Q(1, -1, 0)이므로

$\vec{PX} +\vec{QX} = (x-1, y+1,z-2)$ $+ (x-1, y+1, z) = 2(x-1, y+1, z-1)$이되고

그러면 $|\vec{PX}+\vec{QX}|^2$=$4{(x-1)^2+4(y+1)^2+4(z-1)^2}$이됩니다. 그러므로 점 $X$와 $A(1, -1, 1)$사이의 거리가 가장 먼 거리를 구하면됩니다. 

 

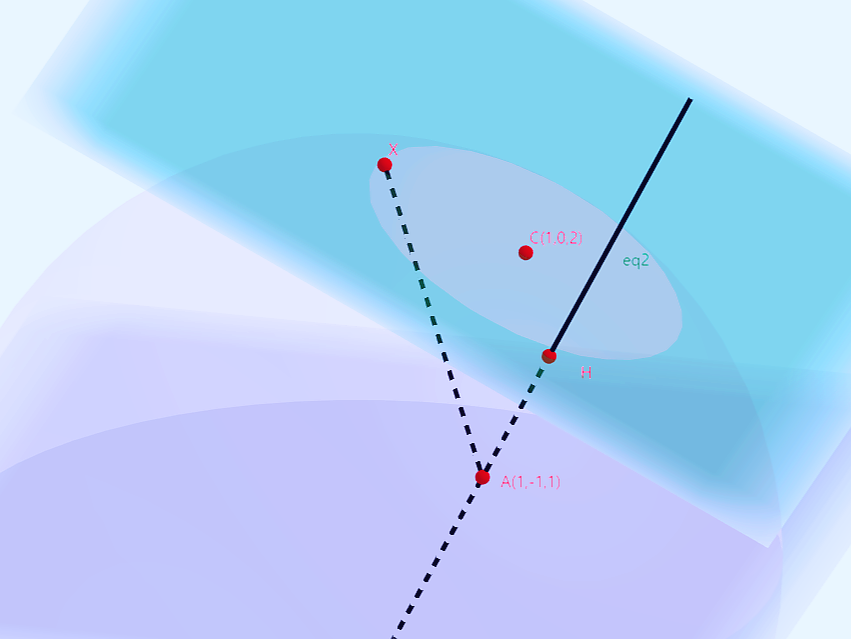
점$A(1, -1, 1)$와 평면 $x+2z-5=0$ 사이의 거리를 구하면

$\overline{AH} = \frac{|1+2-5|}{\sqrt{1+4}} = \frac{2}{\sqrt{5}}$

$\overline{AC} =\sqrt{1^2+1^2} = \sqrt{2}$ 

$\overline{CH}^2 = \overline{AH}^2-\overline{AC}^2 = \frac65$

저희가 구하려는 값은 $|\vec{PX}+\vec{QX}|^2$=$4{(x-1)^2+4(y+1)^2+4(z-1)^2}= 4\overline{AX}^2_{MAX}$ 입니다.

그러므로 삼각형 XAH에서 $\overline{AX}^2_{MAX} = {\overline{XH}_{MAX}}^2+\overline{AH}^2$ $=\lbrace1+\sqrt{\frac65}\rbrace^2+\lbrace\frac{2}{\sqrt{5}}\rbrace^2=3+\frac25\sqrt{30}$ 이 됩니다.

그러므로 $4\overline{AX}^2_{MAX} =12+\frac85\sqrt{30}$ 입니다.

$a = 12$ 이고 $b = \frac85$이므로

$10(a+b) = 10(12+\frac85) = 136$

 

 

30번입니다.

$f(x)$그래프는 저희가 잘 아는 그래프이고 발문에서 어떤 홀수 $k$라고하였으므로, 가장 쉬운 숫자 1을 넣겠습니다.

그러고 나서 $g(t)$를 살펴보면 적분 값 안이 $f(x)cos({\pi}x)$입니다. 발문의 처음에서 주어졌듯이 $f(x)$는 $t$값에 따라 변하고, $g(t)$함수도 $k$값에 따라 변하므로 $f(x)cos({\pi}x)$를 함수 식으로 풀기에는 복잡합니다. 

그리고 조건 발문에서 $t=\alpha$에서 극솟값 이라고 하였으므로, 저희는 함숫값이 작아지는 순간의 점만 조사해보면 됩니다. 이 까지의 발문에 명시되어있는 단어를 토대로 저희는 이 문제를 식으로 풀어야 하는 것이 아니라 그림으로 풀어야 한다 는 것을 발문을 통해 알 수 있습니다. 발문에서 어떤 홀수 $k$라하였으므로, $k$에는 가장 쉬운 숫자 1을 넣고, 그에 알맞게 $f(x)$는 $t=1$을 넣어서 그림을 그렸습니다.(왜냐하면 저희는 함숫값이 가장 작아지는 순간의 점을 조사해야 하기 때문에 $t=1$을 넣어 $f(x)$를그리면 $f(x)cos({\pi}x)$가 1에서 가장 작은 함숫값을 가지기 때문입니다.) 그러면 이와 같은 그림이 그려집니다.

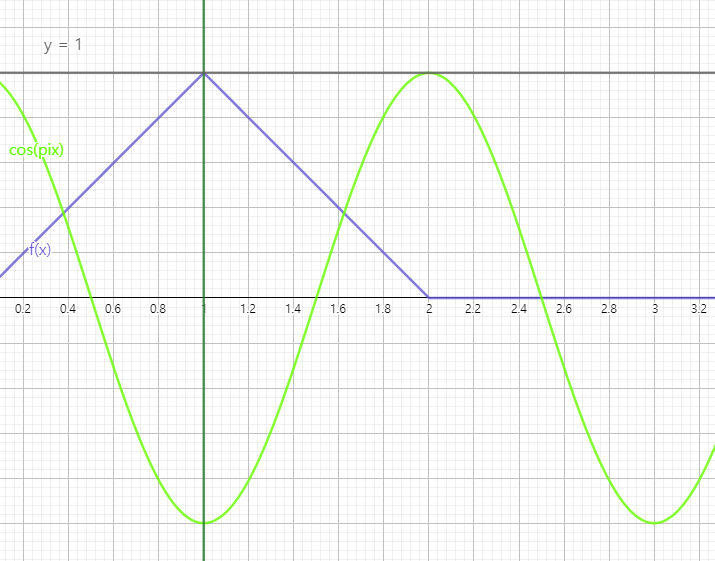
이 그래프에서 저희는 $f(x)cos({\pi}x)$에서  $t$값을 1에서 9까지 넣으면서($k=1$을 넣었으므로 적분 구간은 1~9입니다.) 극솟값을 조사해야합니다.

그리고 그 개수를 조사하면되는데 위의 그림을 보면 $\int_1^{9}$ $f(x)cos({\pi}x)$값이 $x=1$에서 최솟값을 가진다는 것을 알 수 있습니다.( 왜냐하면 $f(x)$는 커지고 $cos({\pi}x)$는 작아 지기 때문입니다.)

대략적인 그림을 그리면 이와 같이 나옵니다.

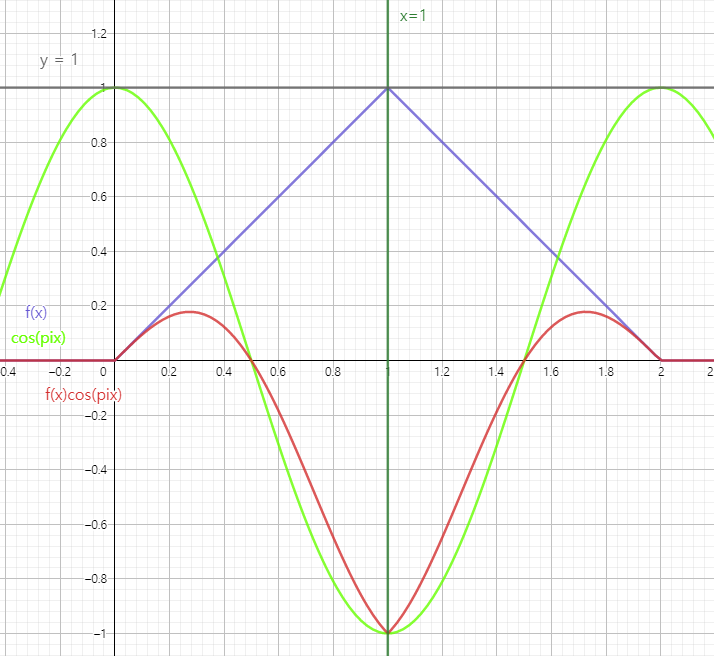
$f(x)cos({\pi}x)$는 빨간 선 그래프처럼 그려지고 이때 넓이가 가장 작으므로 ($f(x)$에 $t=2$를 넣은 그래프와 $t=1$일때를 비교해보면 $t=1$일때 $\int_1^{9}$ $f(x)cos({\pi}x)$값이 극소가 된다는 것을 눈으로 쉽게 확인할 수 있습니다. 아래의 그래프를 봐주세요.)

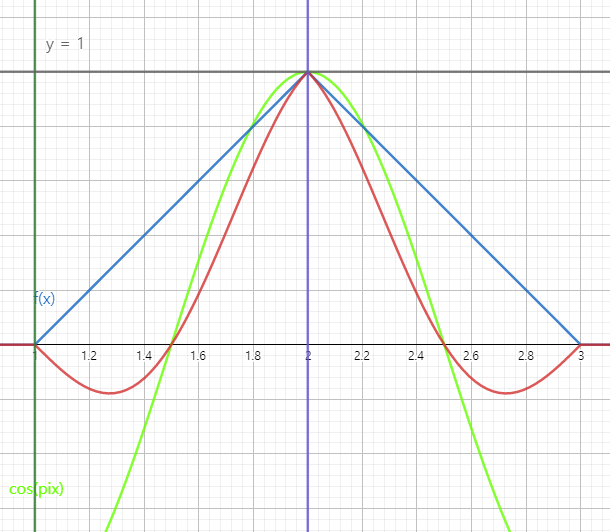
$t=2$일때는 $f(x)cos({\pi}x)$는 빨간색 그래프처럼 그려집니다. 그러므로 적분 값이 양수가 됩니다. 발문에서 원하는 조건에 맞지 않습니다. (문제에서 원하는 조건은 적분 값이 음수입니다. $g(\alpha)<0$) 

그러므로 저희는 홀수 값(1, 3, 5, 7, 9)일 때 $\int_1^{9}$ $f(x)cos({\pi}x)$값이 극소를 가진다는 것을 알 수 있습니다.

$t=1$을 넣었으므로 즉 $k$, $k+2$, $k+4$, $k+6$, $k+8$일때 극소값을 가집니다.

 

 

그러므로 $ m = 5$가되고 $\sum_{i=1}^n \alpha_i = 5k + 25 =45$이므로 $k=5$가 됩니다.

계산을 간단하게 하기 위해 $t=1$을 넣고 $k-\pi^2\sum_{i=1}^mg(\alpha_i)$을 계산하면

$5$ $- \pi^2 \lbrace g(\alpha_1)+g(\alpha_2)+g(\alpha_3)+g(\alpha_4)+g(\alpha_5) \rbrace$

$cos({\pi}x)$의 대칭성을 이용하여

$g(\alpha_1) = g(\alpha_5)$ $= \int_0^{1}$ $f(x)cos({\pi}x)dx = \int_0^{1} xcos({\pi}x)dx = -\frac{2}{\pi^2}$

 

$g(\alpha_2) = g(\alpha_3) = g(\alpha_4)$ $= \int_0^{2}$ $f(x)cos({\pi}x)dx = 2\int_0^{1} f(x)cos({\pi}x)dx = -\frac{4}{\pi^2}$

그러므로 $5$ $- \pi^2 \lbrace g(\alpha_1) + g(\alpha_2) + g(\alpha_3) + g(\alpha_4) + g(\alpha_5) \rbrace $ $= 21$

그러므로 정답은 21이 됩니다.

복잡해 보이는 문제였지만 발문의 순서대로 풀어보면 그리 어렵지 않게 풀리는 문제였습니다. 이 문제에서 얻어갈 것 어떤 홀수, 실수 t에 관하여라는 표현은 너무 광범위하므로 조건에 맞게 쉬운 숫자를 넣으면 문제를 이해하기에도 계산하기에도 훨씬 수월해진다는 것입니다.

그럼 지금까지 2018 대학 수학능력 시험 수학 가형 29번 30번 풀이를 마치겠습니다.

나머지 문제풀이를 원하시는 분은 댓글 남겨주시면 바로 올려드리겠습니다. 읽어주셔서 감사합니다.

 

2018수능 수학 가형 21번 풀이

수능(모의고사) - 2018학년도 대학수학능력시험(수능) 수학 가형(짝수) 21번 문제 풀이