안녕하세요
푸디헬스입니다
오늘은 중심 극한 정리(CLT : Central Limit Theorem)의 코드를 짜 보고 눈으로 확인해보겠습니다.
중심 극한 정리는 확률론이나 통계를 배우신 적이 있는 분이라면 한 번쯤은 들어보셨을 것입니다.
그럼 중심 극한 정리는 무엇일까요?
쉽게 설명하면 어떤 모집단의 표본이 충분히 크다면 표본 평균의 분포는 정규분포를 따른다는 것입니다.
그럼 확률분포의 표본이 많을수록, 표본 평균이 정규 본포에 근사하다는 것을 눈으로 확인해 보겠습니다.
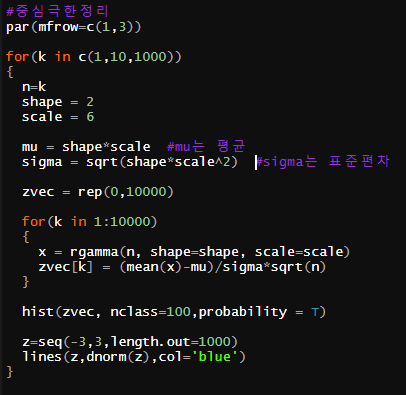
par(mfrow = c(1,3)) : plot의 그림을 1행 3열로 지정하는 옵션입니다. plot에 3개의 그림을 한 번에 볼 수 있어요
Chapter 16 - 대수의 법칙에서 대수의 법칙 코딩 예시와 같이 이번에도 gamma분포를 따를 때 코딩을 짜보았습니다.
gamma분포 : shape * scale = 평균
shape * scale^2 = 분산
mu : 평균
sigma : 표준편차
zvec = rep(0,10000) : 0이 10000개 있는 벡터 생성
for(k in c(1, 10, 1000)) : 모집단의 표본을 1개 10개 1000개로 늘려나가면서 반복문을 실행합니다.
n : 표본
for(k in 1:10000) 구문 : 10000번을 실행합니다.
그리고 zvec에 표준화된 데이터를 넣습니다.
hist(zvec, nclass = 100, probability = T) : 표준화되어있는 데이터의 히스토그램을 그리는데 옵션이 구간을 100개(nclass = 100) 높이는 확률(probability = T)로 그려줍니다.
그리고 z = seq(-3, 3, length.out = 100) : -3~3까지 100등 분해 x축의 실수를 만들어주고
lines(z, dnorm(z), col = 'blue') : lines함수로 표준화되어있는 데이터의 histogram위에 정규분포를 파란색으로 그려 비교해봅니다.
그러면 그 결과는!
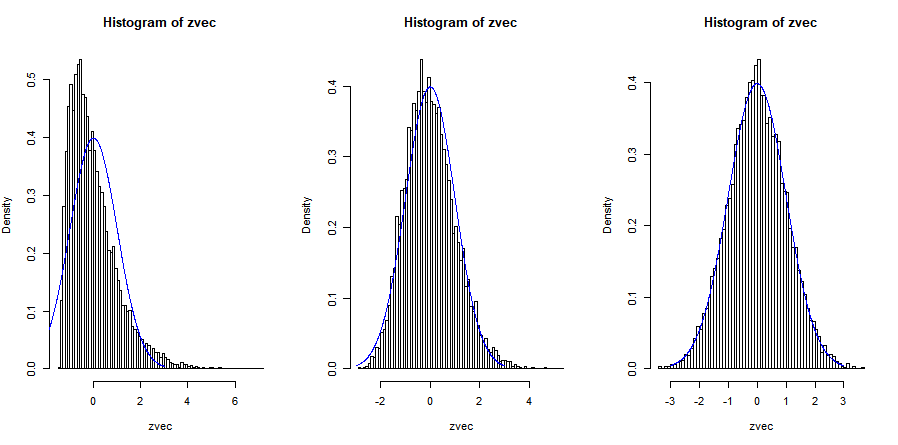
왼쪽에서 오른쪽으로 순서대로 표본이 1 10 1000일 때입니다.
표본이 커질수록 표본 평균이 정규분포(파란색)에 가까워진다는 것을 눈으로 확인할 수 있습니다.
중심 극한 정리의 증명은 적률 생성 함수를 이용해서 증명할 수도 있습니다.
하지만 복잡한 수학적 수식보다는 시각적으로 확인하는 게 더 이해하기 쉽다고 생각해요. 그래서 이 코드를 직접 한 번 짜 보시면 잘 까먹지 않을 거라고 생각합니다^^
그럼 오늘은 중심 극한 정리(CLT : Central Limit Theorem)를 코딩해보고 눈으로 확인해보았습니다.
중심 극한 정리는 확률이나 통계에 아주 중요한 부분을 차지하니 꼭 한번 직접 해보시길 권합니다.
궁금한 거 있으시면 댓글 달아주시고
(회기역 근처에서 R 기초 과외하고 있으니 관심 있으신 분은 jwj4519@naver.com 또는 jwj4519(카톡 ID)로
연락 주세요^^)
좋은 하루 보내세요^^




댓글