안녕하세요. 푸디헬스입니다.
수학 공부를 하는데 어떻게 공부를 해야 좀 더 효율적으로 할 수 있는지 고민하시는 분들이 계실 겁니다.(어떻게 하면 적은 시간으로 빠르고 정확하게 문제를 풀 수 있을까?) 수학은 암기과목과 달리 외우기만 해서는 안되니깐 문제를 많이 풀어야 한다고 생각하시는 분도 있고, 암기과목처럼 유형을 달달 외우는 분들도 있을 겁니다. 어떤 방법이 정답이라고 할 수는 없지만, 수능을 준비하는 수험생이라면 단순히 문제만 많이 푼다고 수학 성적이 오르진 않을 겁니다. 그럼 수학 공부를 어떻게 하는 것이 가장 효율적일까요?

수능을 위한 제가 생각하는 가장 효율적인 수학 공부는 필요한 공식과 개념을 정리하고 공식을 정확하게 암기하고 있는 것입니다. 이런 식으로 말이죠. 제가 수학 공부할 때 정리하는 방식입니다.
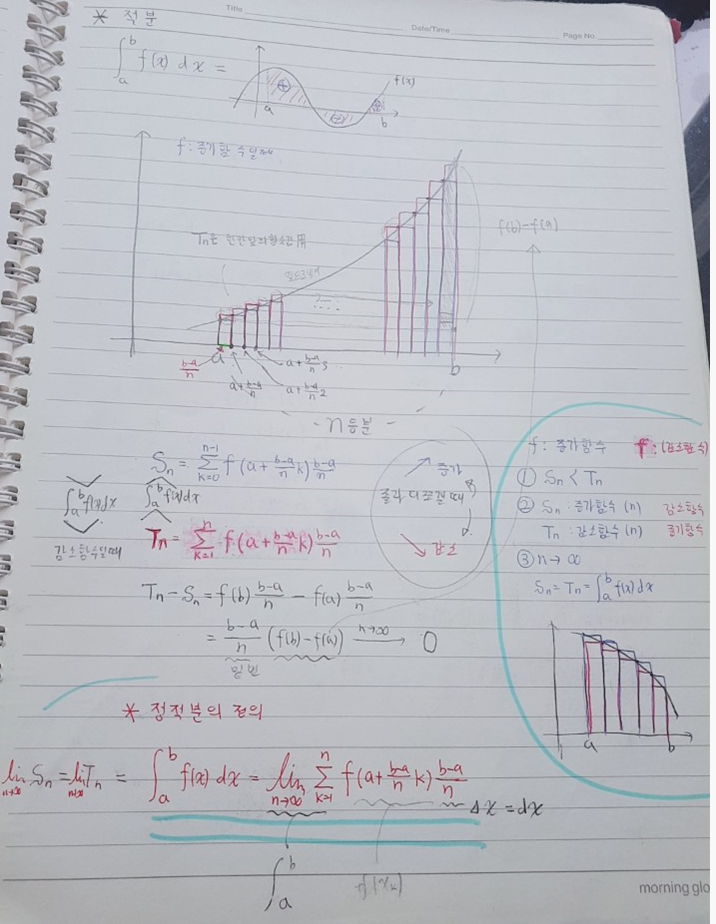
적분의 개념에 대해 정리한 것입니다.

수학 모의고사를 푸는데 필요한 공식을 정리한 것입니다.
이런 식으로 수학 개념을 정리하면 한눈에 알아보기 쉽고, 개념 정리를 하는 것이기 때문에 개념 이해에 도움이 되며, 수학 문제를 푸는데 필요한 공식을 정리하면 암기와 동시에, 어떤 단원에서 어떤 것들을 외워야 하는지 한눈에 알아볼 수 있어 단원 정리 및 암기에 도움이 많이 됩니다. 단순히 수학 문제를 많이 풀거나 모든 수학 유형을 정리하기에는 그 양이 너무 방대하기 때문에 한계가 있습니다. 그러므로 수능 수학 공부를 하시는 수험생분들 중 수학 공부를 어떻게 해야 하는지 갈피가 잘 잡히지 않는 분은 위의 방법을 한번 해보시는 것을 권장드립니다. 그럼 2018 9월 모의고사 얘기로 넘어가겠습니다.
2017 9월 6일 수요일 평가원이 주관한 대학 수학능력시험 9월 모의평가입니다. 1등급 컷은 91점이고 등급컷이 92쯤에 형성된 잘 치러진 시험이었습니다. 이번 시험에서도 오답률 1위는 30번으로 96%, 오답률 2위는 29번으로 88%를 차지했습니다. (21번(60%), 20번(53%), 27번(45%)이 그다음으로 오답률이 높은 문제였습니다.)
그럼 29번을 풀어보겠습니다.

벡터와 3차원 좌표평면 관련 문제입니다. 어느 때와 같이 발문의 순서대로 문제를 풀어보겠습니다.

$\vec{OB}\cdot\vec{OP}=0$이므로 점 $P$는 $xy평면$위의 점이고, $|\vec{OP}|<=4$이므로 원점을 중심으로 하고 반지름이 4인 원인 것을 알 수 있습니다. 이를 그림으로 3차원 좌표평면에 나타내면 이와 같이 표현됩니다.
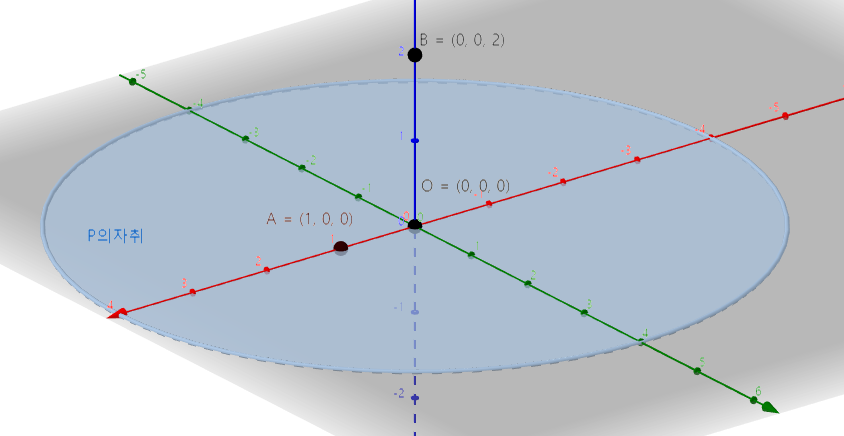
그다음 조건을 살펴보겠습니다

$\vec{PQ}=1$에서 $점Q$가 $점P$를 중심으로 하고 반지름이 1인 구를 의미한다는 것을 알 수 있습니다.. 그리고 발문에서 조건을 위와 같이 제시해주었으므로, 발문에서 시키는 대로 조건을 활용합니다. 그러면 $\vec{PQ}=1$이고 $\vec{PQ}\cdot\vec{OA}=|\vec{PQ}||\vec{OA}|cos\theta$$=1\times1\times cos\theta>=\frac{\sqrt{3}}2$가 됩니다.
그러므로 $0<=theta<=30$이됩니다. ($\vec{OA}$방향은 x축방향입니다. 그러므로 x축방향과 이루는 각이 30˚가됩니다.)
이제 이를 $점Q$의 자취를 그려보면 x축과 30˚를 이루므로 임의의 점 $P$를 잡았을 때 그림으로 표현해보면 아래와 같이 그려집니다.
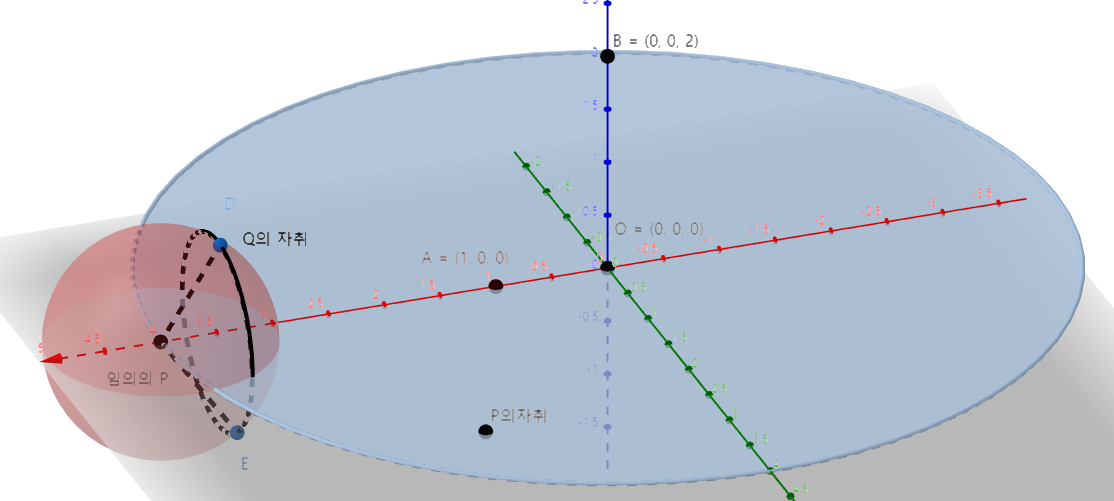
이제 여기서 $|\vec{BQ}|$의 최댓값과 최솟값을 구해야합니다. 그러면 $|\vec{BQ}|$의 최댓값은 위의 그림에서 $\overline{BP}$의 길이에다가 반지름 1을 더한 값(왜냐하면 점B와 점P와 점Q가 일직선일 때 최대가 되기 때문입니다.)이라는 것을 쉽게 알 수 있습니다.
그러므로 최댓값은 $점B (0,0,2)$와 $점P (4,0,0)$의 거리에다가 반지름 1을 더한 값 이므로 $2\sqrt{5}+1$이됩니다.
그리고 $|\vec{BQ}|$의 최솟값은 아래의 그림과 같이 그려질 때라는 것을 알 수 있습니다.
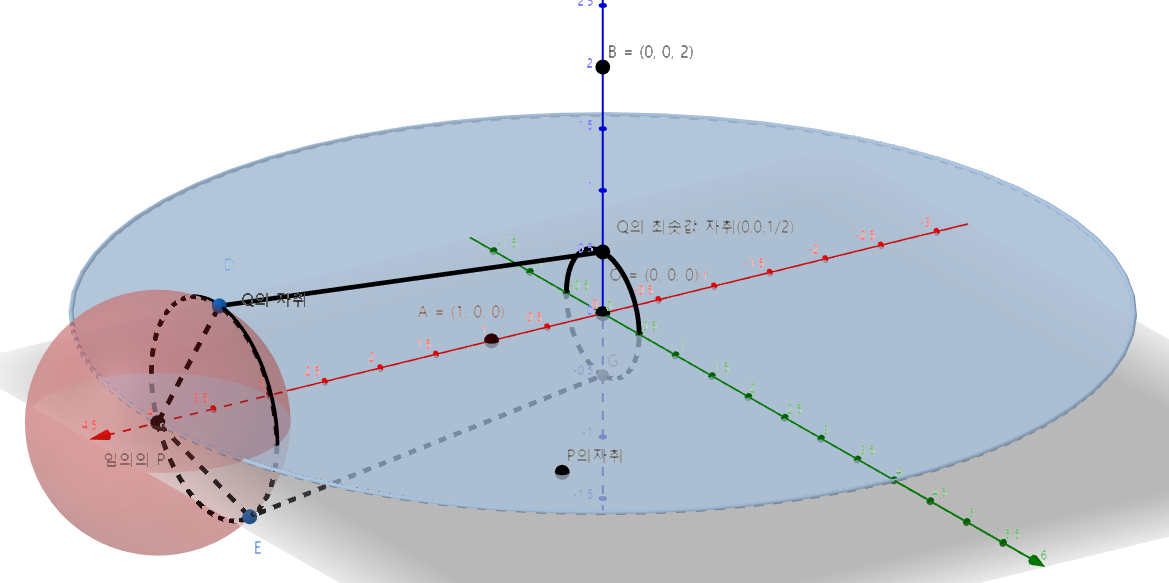
여기서 Q의 반지름은 구의 반지름이 1이고 각도가 30˚이므로 Q의 자취의 반지름은 $\frac12$것을 알 수 있습니다.
그러므로 $|\vec{BQ}|$의 최솟값은 $2-\frac12=\frac32$이 됩니다.

그러므로 $M+m =2\sqrt{5}+1+\frac32=\frac52+2\sqrt{5}$가 되고 $a=\frac52, b=2$가되어 정답은
$6(\frac52+2)=27$이됩니다.
발문의 순서대로 풀면 그리 어렵지 않은 문제였습니다. 잘 이해가 가지 않거나 다른 문제의 풀이가 궁금하신 분은 댓글을 남겨주시기 바랍니다. 감사합니다.
2018 고3 대학수학능력시험 9월 모의고사 수학 가형 30번
모의고사 - 2018 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 가형 30번 풀이
안녕하세요. 푸디헬스입니다. 수학시험을 볼 때 가져야 할 태도는 어떤 게 있을까요? 여기서 태도라고 하는 것은 가장 좋은 점수를 받는 태도를 의미합니다. 수학시험에는 30문제를 푸는 데 100분이 주어집니다...
foodiehealth.tistory.com
2018 고3 대학수학능력시험 9월 모의고사 수학 가형 21번
모의고사 - 2018 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 가형 21번 풀이
안녕하세요. 푸디헬스입니다. 2018년 9월 5일 수요일 평가원이 주관한 대학수학능력시험 9월 모의평가 수학 가형 21번입니다. 이번 모의고사에서 오답률 60%로 3위를 차지했던 문제입니다. 발문을 처음부터 끝가..
foodiehealth.tistory.com




댓글