2020 9월 수학가형 21번(고3 대학수학능력시험 9월 모의평가 : 모의고사)

2020_고3_9월모의평가_수학 가형.pdf

0.45MB

2020_고3_9월모의평가_수학가형_답지.pdf

0.04MB

안녕하세요. 푸디헬스입니다.

2019년 9월 4일 수요일 한국교육과정평가원의 주관하에 2020 고3 대학수학능력시험 9월 모의평가가 치러졌습니다.

그중 21번은 출제자의 의도를 파악하지 못한 수험생분이 있거나, 혹은 파악했더라도 정답을 내지 못한 수험생들이 있었습니다. 하지만 21번은 발문에서 출제진들이 적나라하게 풀이 방법을 알려주고 있습니다. 

그럼 21번을 풀어보겠습니다.

발문은 너무나도 간단합니다. 점 $A(-2, 0), B(2,0)$을 제시해주고, 직사각형 위를 움직이는 점 $P$에 대하여

$\overline{PA} + \overline{PB}$의 값을 물었고 점 $P(0,6)$일때 최대 $(\frac52, \frac32)$일 때 최소라고 하였습니다.

그럼 이것을 그림으로 그려보겠습니다.

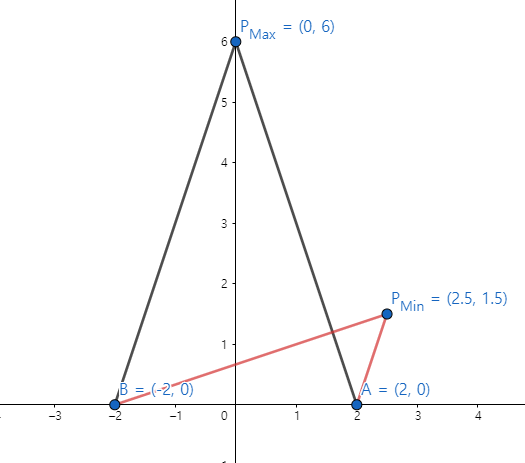
발문에서 문제풀이를 알려주는 부분은 $\overline{PA} + \overline{PB}$라고 명시되어 있는 부분입니다.

두 정점과 다른 한 점과의 거리의 합입니다. 그러면 저희는 당연히 이와 관련된 개념인 당연히 타원을 떠올립니다. 왜냐하면 타원의 정의는 두 정점에서 거리의 합이 일정한 점들의 집합이기 때문입니다.

그럼 이 문제에서 초점이 점 $A(2,0), B(-2,0)$이고 점 $P_{Max}$인 타원과, 점 $P_{Min}$를 지나는 타원이 나옵니다.

초점이 $x축$위에 있으므로 타원의 방정식은 $\frac{x^2}{a} + \frac{y^2}{b} = 1$이고 

$\overline{PA} + \overline{PB} =2a$임으로

$\overline{P_{Max}A}+\overline{P_{Max}B}$ = $2\sqrt{6^2+2^2} = 2\sqrt{40} = 2a$

$a = \sqrt{40}$, $ a^2 = 40$임으로 $\frac{x^2}{40}+\frac{y^2}{36}=1$이되고

$\overline{P_{Min}B}+\overline{P_{Min}A}$ = $\sqrt{(\frac52)+2)^2+(\frac32)^2}+\sqrt{(\frac52-2)^2+(\frac32)^2}$ = $\frac{\sqrt{10}}{2}+\frac{3\sqrt{10}}{2}$ = $2\sqrt{10} = 2a$임으로 $a=\sqrt{10}$이고

$\frac{x^2}{10}+\frac{y^2}{6}=1$이됩니다.

 

 

 

 

이를 그림으로 표현하면 이와 같이 나옵니다.

그런데 점 $P$는 직사각형 위의 점이라고 하였고 직사각형의 넓이가 최대일 때가 $P_{Max}$ 최소일 때가 $P_{Min}임으로 빨간 타원과 파란 타원과 만나는 직사각형의 점은 각각 $P_{Max}$와 $P_{Min}$으로 유일해야 합니다. 그러므로 이와 같이 그러 져야 합니다.

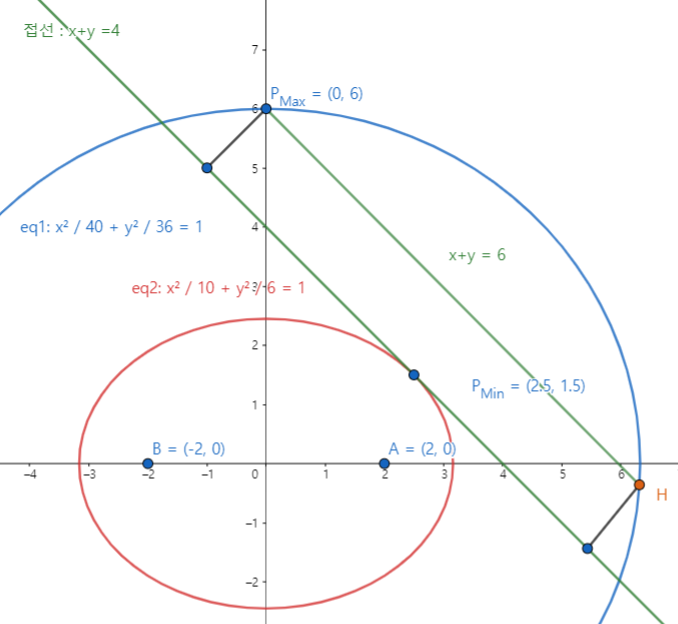
$\frac{x^2}{10}+\frac{y^2}{6}=1$의 $P_{Min}(\frac52,\frac32)$에서의 접선은 타원 위의 점에서의 접선의 공식에 의해 $\frac{1}{10} \frac52 x + \frac16 \frac32 y = 1$ 정리하면 $x+ y = 4$가됩니다.

직사각형의 넓이를 구해야 하므로 점 $H$를 구해야 합니다. 점 $P$와 점 $H$를 지나는 직선은 $x+ y = 4$와 평행이므로 $x + y = 6$이됩니다.($y$절편 = $P_{Max}(0,6)$) 

점 $H$는 타원 $\frac{x^2}{40}+\frac{y^2}{36}=1$과 직선 $x + y = 6$의 교점이므로 $y = 6-x$를 넣고 계산하면,

$\frac{x^2}{40} + \frac{x^2-12x+36}{36} = 1$이되고 정리하면 $\frac{1}{40}x^2+\frac{x^2}{36}-\frac13 x = 0$

$\frac{19}{10}x^2 -12x = 0$, $x(\frac{19}{10}x-12) = 0$, $x = \frac{120}{19}$이 됩니다.

직선의 기울기가 $1$임으로 $직사각형의 가로길이$ = $\overline{P_{Max}H} =\frac{120}{19} \sqrt2 $가되고

직사각형의 세로길이는 직선 $x + y = 4$와 점 $P_{Max}(0,6)$사이의 거리임으로 $직사각형의 세로길이$ = $\frac{|4-6|}{\sqrt2}=\sqrt2$ 

그러므로 직사각형의 넓이는 $\frac{120}{19} \sqrt2 \times \sqrt2 = \frac{240}{19}$이되고 정답은 ⑤입니다.

 

$\overline{PA} + \overline{PB}$를 보고 타원만 떠올릴 수 있다면 어렵지 않은 문제였습니다.

잘 이해가 가지 않거나 다른 문제의 풀이가 궁금하신 분은 댓글을 남겨주시기 바랍니다. 감사합니다.

 

 

2020 고3 대학 수학능력시험 9월 모의고사 수학 가형 29번 풀이입니다.

모의고사 - 2020 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 가형 29번 풀이

 

2020 고3 대학 수학능력시험 9월 모의고사 수학 가형 30번 풀이입니다.

모의고사 - 2020 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 가형 30번 풀이