2018 수능수학가형 21번 짝수형 문제풀이(대학수학능력시험)

2018수능 수학 가형(짝수).pdf

0.54MB

2018수능 수학 가형(짝수)_답지.pdf

0.08MB

안녕하세요. 푸디헬스입니다.

2017학년도 11월 23일 목요일 시행되었던 시험입니다. 1등급(5.13%)컷은 92점에 형성된 잘 치뤄진 시험이었습니다. 

오답률 1위는 95%로 30번, 2위는 94%로 29번, 3위는 72%로 21번이 차지했습니다.

그럼 21번 문제를 풀어보겠습니다.

발문순서대로 읽으면서 문제를 풀어보겠습니다.

발문에서 ~일 때라는 단어가 나오면 그 발문 전까지 문제를 해석하고 다음으로 넘어가는 것이 좋습니다. (그 전까지 이해를 하고 넘어가라는 평가원의 표현의 언어입니다.)

양수 $t$에 대해 $f(x)$가 위와같이 저희가 잘 아는 함수로 정의되어 있으므로 그래프를 그려봅니다.

함수 $ln(x)$를 $1\le x <e $에서는 그대로 그려주고

함수 $x \ge e$에서는 함수 $ln(x)$를 양수 $t$에 대해 $-t$만큼 평행이동한 함수를 그려줍니다.

 

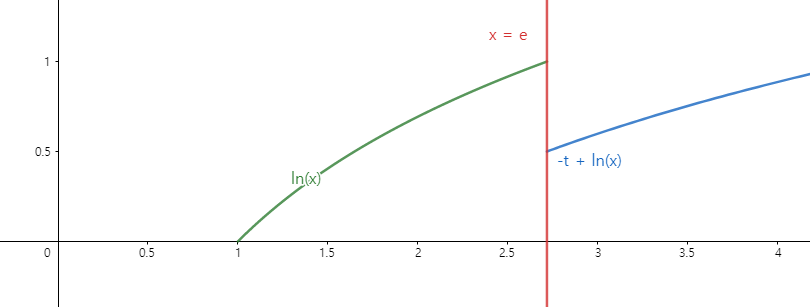
그리고 나서 1 이상의 모든 실수 x에 대하여 (x-e){g(x)-f(x)} \ge 0이다. 를 만족하는 일차함수 $g(x)$중 직선 $y = g(x)$의 기울기의 최솟값을 $h(t)$라고 하였습니다.

$ (x - e) {g(x) - f(x)} \ge 0$

발문에서 $f(x)$의 함수의 범위가 나누어져있으므로 당연히 조건도 범위를 나누어줍니다.

$1 \le x <e$일때 $g(x) \le f(x)$

$x \ge e$일때 $g(x) \ge f(x)$

즉 $1 \le x <e$일때, 직선이 곡선보다 아래에 있고, $x \ge e$일때 직선이 곡선 위에 있어야 합니다. 이를 그림으로 나타내면 이와같이 됩니다.

 

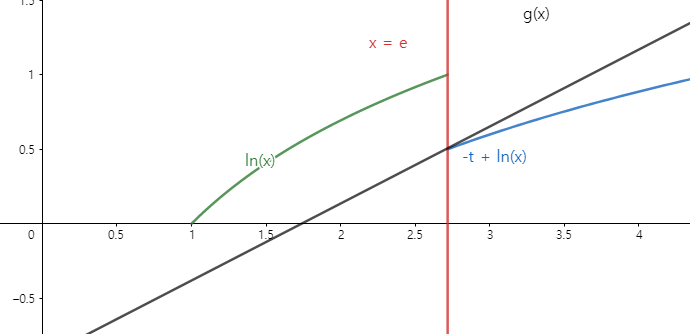
여기서 $-t + ln(x)$그래프를 $t$값이 0에서부터 값을 키워가며 관찰해보겠습니다. 그러면 $t$값이 아주 작을때 즉 $ln(x)$와 차이가 거의 없을때를 고려해보면, $g(x)$의 기울기의 최솟값은 점 $(1,0)$과 $(e, 1-t)$를 지날 때라는 것을 알 수 있습니다.

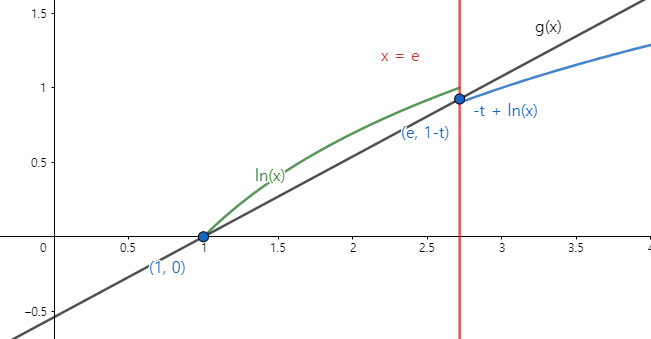
여기서 $-t + ln(x)$그래프의 점 $(e, 1-t)$에서의 접선은 초록 그래프인 $ln(x)$를 자르고 지나가는 것을 그림으로 봐도 알 수 있습니다. 그러므로 $t$값이 일정이상 커지게 되어 점 $(e, 1-t)$에서의 접선이 점 $(1, 0)$을 지날때가 $t$값의 경계값이 됨을 알 수 있습니다.

즉 $h(t)$는 점 $(1, 0)$과 점 $(e, 1-t)$의 기울기이므로

$ h(t) = \frac{1-t}{e-1}$

$f'(e) = \frac{1}{e}$

$\frac{1-t}{e-1} = \frac{1}{e}$일때 $t = \frac{1}{e}$가 나옵니다.

이를 정리하면

$h(t) = \frac{1-t}{e-1} ( 0< t < \frac{1}{e})$

 

구하려는 값은 $h'(\frac{1}{2e})$와 $h'(a)$이고, $\frac{1}{2e}< \frac{1}{e}$임으로, 

$h(t) = \frac{1-t}{e-1} ( 0< t < \frac{1}{e})$

$h'(t) = -\frac{1}{e-1} = h'(\frac{1}{2e})$

그리고 $h(a) = \frac{1}{e+2}$가 되는 $a$를 구해야하므로, $\frac{1}{e+2}<\frac{1}{e}$이므로

$t \ge \frac{1}{e}$일때 입니다. 그림으로 나타내면 이와 같을 때입니다.

접점 $P(p, ln(p)-t)$에서의 접선의 방정식이 점 $(1, 0)$을 지나야하므로 접선의 방정식

$y = \frac{1}{p}(x-p) +ln(p)-t$ 에다가 $(1, 0)$을 대입하면

$0 = \frac{1}{p} (1 - p) + ln(p) - t$

$1- \frac{1}{p}  = ln(p) - t$이고 $h(t) = \frac{1}{p}$이므로

$1- h(t) = -ln( h(t)) - t$가 됩니다. $h'(a)$를 구해야하므로 양변을 미분하면

$-h'(t) = -\frac{h'(t)}{h(t)} -1$ 여기서 $t = a$를 대입하면

$h'(a) = \frac{h'(a)}{h(a)}+1$ 이고 $h(a) = \frac{1}{e+2}$임으로 정리하면

$ ∴ h'(a) = -\frac{1}{e+1}$이 됩니다.

그러므로

$h'(\frac{1}{2e}) \times h'(a) = -\frac{1}{e-1} \times -\frac{1}{e+1}$ = $\frac{1}{(e-1)(e+1)}$임으로 정답은 ④이됩니다.

 

 

2018학년도 대학수학능력시험(수능) 수학 가형(짝수) 29, 30번 문제 풀이( 오답률 95%, 94%)

수능(모의고사) - 2018 대학수학능력시험 수학 가형(짝수)