2020 9월 수학나형 21번 짝수형(고3 대학수학능력시험 9월 모의평가 :모의고사)

2020_고3_9월모의고사_수학 나형.pdf

0.60MB

2020_고3_9월모의고사_수학나형_답지.pdf

0.04MB

2019년 9월 4일 수요일 한국교육과정평가원의 주관하에 치러진 시험입니다. 만점 ~ 1등급 사이 분들의 오답률 1위는 30번, 2위는 28번, 3위는 21번이 차지했습니다. 1등급 컷은 88점이었습니다. ( 등급별 오답률과 등급컷은 메가스터디 홈페이지에서 확인하실 수 있습니다.) 

메가스터디 :: 합격 불변의 법칙

킬러 문항의 난이도는 낮아졌고, 준킬러 문항의 난이도는 높아졌습니다. 즉, 실수를 줄이고 비교적 쉬운 문제는 빠르고 정확하게 푸는 것이 중요해졌습니다. 수험생분들께서는 개념을 정확하게 외우고, 비교적 쉬운 단원은 실수하지 않게 체화시키는 과정이 필요하다고 생각합니다. 그럼 21번 문제를 풀어보겠습니다.

함 수 $f(x)$가주어지고 $g(x)$를 정의했습니다. 그리고 $<보기>$의 참거짓을 판단하는 문제입니다.

 

$ㄱ.$ 함수 $h(x) = (x-1)f(x)$  → $h'(x) = g(x)$

$h'(x) = f(x) + (x-1)f'(x) = g(x)$   참

 

$ㄴ.$ 함수 $f(x)$가 x = -1에서 극값 0을 가지면 → $\int_0^{1} g(x)dx = -1$

↔ $f(-1) = 0$이고 $f'(-1) = 0$ →$\int_0^{1} g(x)dx = -1$

$f(x) = x^3+x^2+ax+b$이고 $f'(x) = 3x^2 + 2x + a$

$f(-1) = -1 + 1 -a + b = 0$

$f'(-1) = 3 -2 + a = 0$

$a = -1, b = -1$, $f(x) = x^3 + x^2-x-1$

$\int_0^{1} g(x)dx = \int_0^{1} f(x) + (x-1)f'(x)$ = $\int_0^{1} (x^3 + x^2 +x -1) + (x-1)(3x^2+2x-1) dx$ = $\int_0^{1} 4x^3-4x \ dx = 1-2 = -1$  참

 

$ㄷ.$ $f(0) = 0$이면 방정식 $g(x) = 0$은 열린구간 $(0,1)$에서 적어도 하나의 실근을 갖는다.

$ㄱ, ㄴ, ㄷ$문제에서는 앞의 보기($ㄱ$이나 $ㄴ$)가 뒤의 보기에 사용되는 경우가 많습니다.

$ㄱ$에서 $h(x) = (x-1)f(x)$ 일 때  ······ ①

$h'(x) = g(x) = f(x) +(x-1)f'(x)$  ······ ②

 

$f(0)$ = 0$이면 $h(0) = 0$( ∵ ①)

$h(1) = 0$( ∵ ①)

$h'(x) = g(x)$(∵②) 이고 h(x)는 4차 함수(∵ ①)이므로

$g(x)$ = $0 = h'(x)$을 구하면 됩니다.

 

 

그림을 그려보면 아래와 같이 나옵니다.

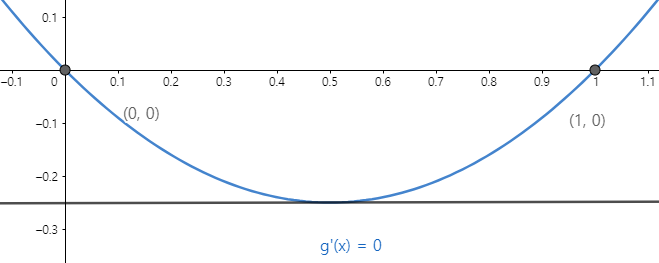
1번 Case

 

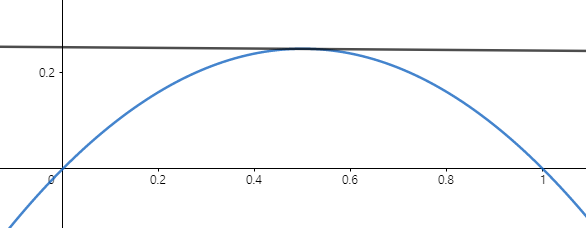
2번 Case

 

 

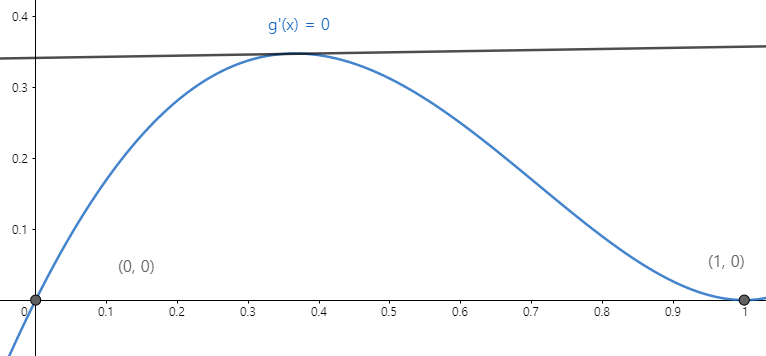
3번 Case

 

어떤 경우든 $g'(x) = 0$이 존재하므로 적어도 열린구간 $(0,1)$에서 적어도 하나의 실근을 가지게 됩니다. 그러므로 $ㄷ.$은 참

그러므로 정답은 ⑤이 됩니다.

오답률이 높지는 않은 문제였지만, 참 거짓 문제를 풀 때 접근하는 방식을 알려주는 좋은 문제였습니다. 

 

 

2020 고3 대학수학능력시험 9월모의고사(모의평가) 수학 나형 29번

2020 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 나형 29번 문제풀이

2020 고3 대학수학능력시험 9월모의고사(모의평가) 수학 나형 30번

2020 고3 대학수학능력시험 9월 모의평가(모의고사) 수학 나형 30번 문제풀이