2020 수능 수학가형 21번 짝수형 (대학수학능력시험)

$f(x)$는 $y = e^x$위의 점 $(t, e^t)$에서의 접선이고,
함수 $y = | f(x) - ln(x) + k| $가 양의 실수 전체의 집합에서 미분 가능하도록 하는 실수 $k$의 최솟값을 $g(t)$라고 하였습니다.
미분 가능하려면 첨점이 생기면 안 됩니다.
즉 $y$축으로 $k$만큼 평행이동하여 $ y = f(x)$와 $ y = ln(x)$가 만나지 않는 최소의 $k$값을 구하면 됩니다.
$k$값인 $g(t)$는 그림에서 보듯이 $y = ln(x)$에서 $f(x)$와 같은 기울기를 가지는 직선을 구해 빨간 직선의 y절편과 y = $f(x)$의 y절편을 비교하면 $g(t)$를 구할 수 있습니다.
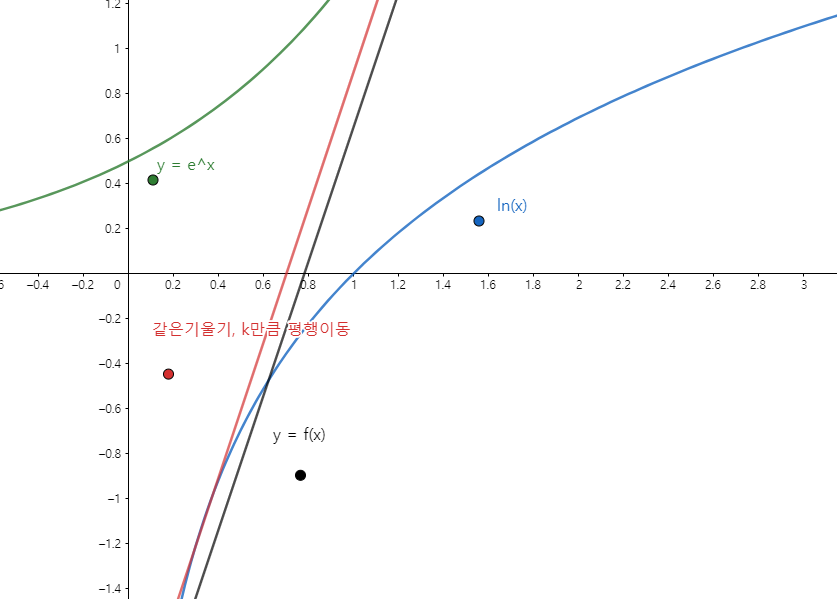
$y = f(x) = e^t(x-t) + e^t$ = $e^tx - t e^t + e^t$ 기울기 $e^t$
$y = ln(x)$미분 $ y = \frac{1}{x} = e^t$이므로 $x = \frac{1}{e^t}$
빨간 직선의 방정식 $y = e^t(x-\frac{1}{e^t}) + ln(e^{-t})$ = $e^tx -1 -t$
$g(t) = (te^t-e^t) - (t + 1)$
그러고 나서 보기를 보겠습니다.

$\int_{a}^{b} g(t) dt = m$
ㄱ. $g(t) < 0$일때가 존재하는지 묻고 있습니다.
$g'(t) = te^t -1$임으로 $te^t = 1$일때 극솟값을 가집니다.
$g(t) = te^t - e^t - t -1$임으로 $te^t = 1$을 대입하면 $g(t) = -e^t -t$로 음수가 나오므로 ㄱ은 참입니다.
ㄴ.
$g(c) = (c-1)e^c-(c+1) = 0$
$c+1 = (c-1)e^c$
$g(-c) = (-c-1)e^{-c} - (-c+1) = -(c+1)e^{-c}+(c-1)$에서 위식을 대입하면
$g(-c) = $-(c-1) + (c-1)$ = 0$
ㄷ. $m$의 값이 최소 일려면 $g(t)$의 모든 음수 부분의 정적분입니다.
한국 교육과정 평가원 문제, 특히 수능 같은 경우의 ㄱ, ㄴ, ㄷ문제는 앞의 보기가 힌트가 되는 경우가 아주 많습니다.
$g'(t) = te^t -1$
$1 + g'(t) = te^t$
$\alpha = -c, \beta = c$
$\frac{1 + g'(\beta)}{1 + g'(\alpha)} = \frac{ce^c}{-ce^{-c}}$ = $-e^{2c}$
그런데 $g(1) = -2$로 음수이고 보기 ㄴ에서 $g(c) =0이면 g(-c) = 0$이 참이었으므로 그림으로 나타내면 아래와 같습니다.
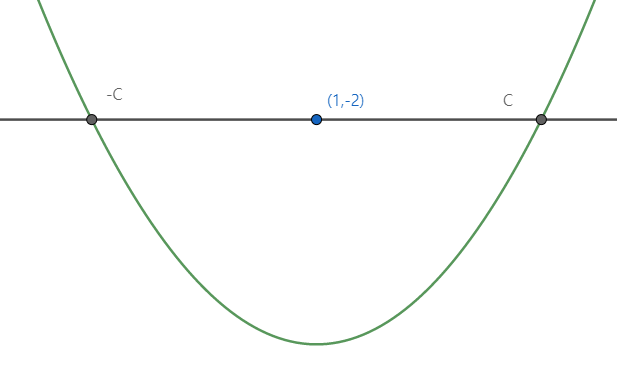
$1 < c$이므로 $2 < 2c$이고 $e^2 < e^{2c}$이므로 $-e^2 < -e^{2c}$가 됩니다.
$\frac{1 + g'(\beta)}{1 + g'(\alpha)} = \frac{ce^c}{-ce^{-c}}$ $<-e^2 <$ $-e^{2c}$
그러므로 ㄷ도 참이 되어 정답은 ⑤이 됩니다.




댓글