지금까지는 약수를 구할 때, 곱하기를 이용해서 구했었습니다.
이제 중학생이 되었으니 조금 더 쉽게 약수를 구해야겠죠?
오늘은 약수를 쉽게 구하는 방법과,
약수를 모두 구하지 않고도 약수의 개수를 구할 수 있는 방법을 배워보겠습니다.
두 가지 방법 모두 저번 시간에 배웠던 소인수분해를 이용해서 구할 수 있습니다.
우리가 해야할 것은 단 2가지입니다.
1. 소인수분해를 한다.
2. 거듭제곱으로 나타낸다.
예시를 통해
바로 시작해 보겠습니다.

소인수분해를 이용하여 약수 구하기
18의 약수를 구해봅시다.
$ 18 = 1 \times 18 = 2 \times 9 = 3 \times 6 $
이므로 18의 약수는 1, 2, 3, 6, 9, 18 총 6개입니다.
그런데 18이 아닌 108과 같은 100이 넘어가는 큰 수라면,
위의 방법처럼 하나씩 약수를 구하기에는 너무 귀찮겠죠?
이럴 때 우리는 소인수분해를 이용하여 약수를 쉽게 구할 수 있습니다.
108을 소인수분해해보면
$ 108 = 2^2 \times 3^3 $이 나옵니다.
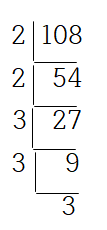
자 그럼 위와 같이 108은 $2^2$과 $3^3$이 곱해진 수라는 걸 알 수 있습니다.
여기서 $2^2$의 약수를 각각 구하고, $3^3$의 약수도 각각 구해서,
서로 곱하면 108의 약수가 됩니다.
그런데 여기서 $2^2$과 $3^3$ 처럼 거듭제곱으로 표현된 수의 약수는
지수를 1씩 늘리면서 쉽게 구할 수 있습니다.
단, 모든 수의 약수인 1은 포함시켜 주어야 합니다.
예를 들면, $2^{50} $ 의 약수는
$1, 2, 2^2, 2^3, ······, 2^{48}, 2^{49}, 2^{50} $이 됩니다.
위와 같은 방식으로 구하면,
$2^2$ 의 약수 : $ 1, 2, 2^2 $
$3^3$ 의 약수 : $1, 3, 3^2, 3^3 $
이제 $ 1, 2, 2^2 $과 $ 1, 3, 3^2, 3^3 $을 각각 곱하면 약수를 구할 수 있습니다.
| $ \times $ | $ 1 $ | $ 2 $ | $ 2^2 $ |
| $ 1 $ | $ 1 $ | $ 2 $ | $ 4 $ |
| $ 3 $ | $ 3 $ | $ 6 $ | $ 12 $ |
| $ 3^2 $ | $ 9 $ | $ 18 $ | $ 36 $ |
| $ 3^3 $ | $ 27 $ | $ 54 $ | $ 108 $ |
표를 보면 곱하기를 이용해 약수를 구한 것과 같습니다.
$ 108 = 1 \times 108 = 2 \times 54 = 4 \times 27 = 3 \times 36 = 6 \times 18 = 9 \times 12 $
$ 108$ 의 약수 : $ 1, 2, 3, 4, 6, 9, 12, 18, 36, 27, 54, 108 $
이렇게 구하는 방법이 처음이라서 낯설고 익숙지 않아
더 복잡해 보일 수 있지만
익숙해지면 곱하기를 이용해 약수를 구하는 것보다
더 정확하고 빠르게 약수를 구할 수 있습니다.
| 소인수분해를 이용해서 약수 구하기 |
| 주어진 수를 소인수분해 후 거듭제곱의 약수를 모두 구하여 서로 곱한다. |
소인수분해를 이용하여 약수의 개수 구하기
이번에는 소인수분해를 이용하여 약수의 개수를 구해보겠습니다.
위에서 구한 것처럼 표를 그릴 필요 없이 약수의 개수만 구하는 거예요.
구하는 방법은 매우 간단합니다.
위의 예시를 보면 $ 108 = 2^2 \times 3^3 $ 입니다.
| $ \times $ | $ 1 $ | $ 2 $ | $ 2^2 $ |
| $ 1 $ | $ 1 $ | $ 2 $ | $ 4 $ |
| $ 3 $ | $ 3 $ | $ 6 $ | $ 12 $ |
| $ 3^2 $ | $ 9 $ | $ 18 $ | $ 36 $ |
| $ 3^3 $ | $ 27 $ | $ 54 $ | $ 108 $ |
여기서 $ 2^2 $ 의 약수의 개수는 $2, 2^2 $에서 1 포함 3개 $ 1, 2, 2^2 $
$ 3^3 $ 의 약수의 개수는 $3, 3^2, 3^3 $에서 1포함 4개 $ 1, 3, 3^2, 3^3 $
즉, 거듭제곱으로 표현된 수의 약수는
지수의 개수보다 1개가 더 많습니다.

$ 108 $의 약수의 개수는 $1, 2, 2^2$과 $1, 3, 3^2, 3^3 $을 각각 곱해서
12개가 나온 것이므로
$ 108 $ 의 약수의 개수는
$ 2^2 $의 약수의 개수 3개
$ 3^3 $의 약수의 개수 4개를 곱한
$ 3 \times 4 = 12 $가 됩니다.
( 표를 보면 이해가 더 쉽습니다. )
정리하면
$ 108 = 2^2 \times 3^3 $에서 2의 지수 2에 1을 더하고, 3의 지수 3에 1을 더해서
$ ( 2 + 1 ) \times ( 3 + 1 ) = 12 $
이해를 돕기 위해 또 다른 예시를 하나 들면,
$ 72 = 2^3 \times 3^2$ 입니다.
약수의 개수는 2의 지수 3에 1을 더하고, 3의 지수 2에 1을 더해서 곱한
$ ( 3 + 1 ) \times ( 2 + 1 ) = 12 $(개)가 되는 거죠.
| 소인수분해를 이용해서 약수 개수 구하기 |
| 각 소인수의 지수에 1을 더해서 서로 곱한다. |
| 소인수분해 → $ a^n \times b^m $ → $ ( n + 1 ) \times ( m + 1) $ |
포스팅 상단에 정리 및 확인 문제가 있습니다.
오늘도 공부하느라 수고하셨습니다.
궁금한 게 있으시면 댓글에 남겨주시기 바랍니다.
감사합니다.




댓글