안녕하세요
오늘은 '최대공약수'에 대해 배워볼텐데요.
이 '최대공약수'라는걸 왜 배워야하는지 부터 알아야겠죠?

예를 들어, 도시를 만들 땅에 구역을 나누다고 합시다.

그런데, 여기서 한 구역을 가로 몇 미터, 세로 몇미터로 잡아야 할지,
몇 개의 구역 ( 몇개의 동으로 )으로 나눌지 잘 모르잖아요?
이 때, 가로 125와 세로 75의 최대공약수인 25를 이용해 아래와 같이 땅을 나누고,

아, 그러면 가장자리 2칸씩 ( 가로 50m, 세로 25m ) 각각 마을 4개로 나누고,
그 가운데 십자가 부분 ( 나머지 부분) 을 도로나, 인도, 상가로 구성하자!
라고 아래와 같이 계획을 세울 수 있겠죠.

이와 같이 최대공약수는 어떤 공간을 어떻게 구성할지 생각하는 단계에서,
공간을 최대공약수로 쪼개 좀 더 구체적으로 계획할 수 있게 도와줄 수도 있고,
조금 더 실생활로 들어가보면,
과자 12개, 음료수 8개를 똑같이 최대한 많은 사람에게 나누어 주는 수를 구하는 방법
을 구해보면
12와 8의 최대공약수인 4
4명에게 1명당 과자 3개, 음료수 2개씩 나누어 주면 됩니다.
재난 상황에서 물자( 먹을거나 생필품 )는 한정 되어있고,
사람수는 많을 때 얼만큼의 양을 나누어 주어야하는지 판단할 때 도움이 되겠죠?
이 외에도 최대공약수를 활용한 다양한 사례가 있지만,
왜 배워야하는지는 이제 알았으니,
최대공약수를 구하는 법을 배워 봅시다.
공약수와 최대공약수
우선 최대공약수를 배우기전에, 말의 의미부터 알아야 해요.
최대공약수 = 최대 + 공약수
최대 = 가장 큰
공약수 = ???
약수는 아는데 공약수는 뭘까요?
공약수는 '두 개 이상의 자연수의 공통인 약수'를 의미합니다.
말로 풀어놓으니깐 잘 모르겠죠?
예시를 들어드릴게요.
'두 개 이상의 자연수' = 12와 18
12의 약수 $ 1, 2, 3, 4, 6, 12 $
18의 약수 $ 1, 2, 3, 6, 9, 18 $
12와 18의 공약수(공통인 약수)는 $ 1, 2, 3, 6 $
이제 좀 이해가 되시나요?
그럼 위의 예시에서 최대인 공약수는??
네 맞아요. $ 6 $입니다.
12와 18의 최대공약수 =$ 6 $
최대공약수는 '공약수 중에서 가장 큰 수'를 의미합니다.
그런데 여기서 이 숫자를 뚫어져라...... 잘 보면?
12와 18와 공약수 = $ 1, 2, 3, 6 $
12와 18의 최대공약수 = $ 6 $
여기에서
'12와 18의 공약수'가 '최대공약수의 약수'인것을 알 수 있어요.
여기서, 한가지 용어만 더 배우면
'서로소' 라는 애가 있는데 이 아이는
'최대공약수가 1인 두 자연수'를 의미해요.
예를 들면,
7의 약수 : 1, 7
6의 약수 : 1, 2, 3 6
공약수가 1밖에없으니
최대공약수도 1이죠?
이러한 두 수 6, 7을 서로소라고 부른답니다.
자 그럼, 한번 정리해봅시다.

최대공약수 구하는 방법
최대공약수를 구하는 방법은 크게 2가지가 있어요.
1. 공약수로 나누기
2. 소인수분해 이용하기
저는 개인적으로 1번을 추천해요.
왜냐하면 1번이 더 쉽고 간단하거든요. ( 본인 생각... )
최대공약수 구하기 첫번째 방법 - 공약수로 나누기
이 방법은 되게 간단해요.
두 수의 공약수로 나누면 됩니다.
언제까지?
두 수의 몫이 서로소가 나올때까지 나누면 됩니다.
그리고 나눈 수들의 곱이 최대공약수가 되죠.
예시로
24와 30의 최대공약수를 구해봅시다.
두 수의 공약수로 나눌 때,
두 수의 공약수를 먼저 찾아야하는데
두 수의 공약수를 찾는 쉬운 방법은
2, 3이 두 수의 공약수인지 확인하면 됩니다.
두 수가 2, 3의 배수인지 확인하는거죠.
2, 3, 5, 7, 11 ······ ( 작은 소수부터 확인 )

만약
두 수의 공약수를 쉽게 찾으실 수 있다면,
2, 3, 5, 7, 11 ······ 처럼 작은 소수부터 나누지 않고,
바로 공약수로 나누어도 됩니다.
24와 30은 6의 배수인게 보이죠?
그러니 6은 24와 30의 공약수입니다.

굳이 소수로 나누지 않아도 최대공약수는 똑같이 나온답니다.
두 수의 공약수 중 큰 수를 찾을 수 있으면 훨씬 계산이 간단해지겠죠?
최대공약수 구하기 두번째 방법 - 소인수분해 이용
두번째 방법은 위에서 말했듯이 소인수분해를 하는거에요.
똑같은 예시로 24와 30을 해봅시다.
24와 30을 소인수분해하면
아래와 같이 되고

거듭제곱으로 표현하면,
$ 24 = 2^3 \times 3 $
$ 30 = 2 \times 3 \times 5 $
여기서 공통인 소인수를 모두 곱하는데,
그 중에서 소인수의 지수가 같으면 그대로, 다르면 작은것을 택하여 곱합니다.
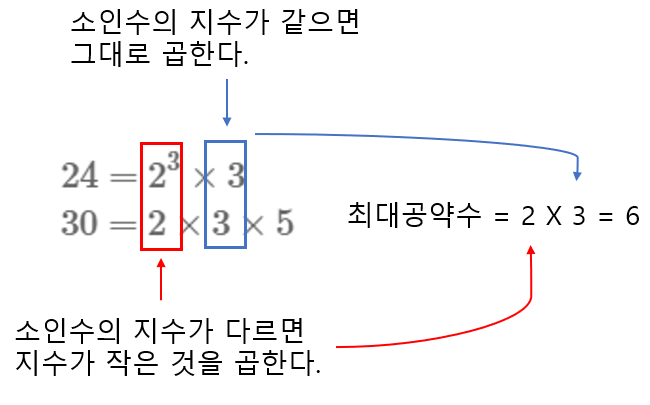
공통인 소인수 2, 3
그 중에서 지수가 작거나 같은것을 택하여 곱하면 됩니다.
이해가 되셨나요?
자, 정리해봅시다.

포스팅 상단에 정리 및 확인 문제가 있습니다.
오늘도 공부하느라 수고하셨습니다.
궁금한 게 있으시면 댓글에 남겨주시기 바랍니다.
감사합니다.




댓글