최대공약수와 최소공배수의 관계
최대공약수와 최소공배수를 구하는 방법에 대해서 잘 이해하셨나요?
구하는 방법은 여러 가지였지만, 대부분의 경우에 소인수분해를 이용해 최대공약수와 최소공배수를 구한답니다.
이번시간에는 최대공약수와 최소공배수 사이에 어떤 관계가 있는지 알아볼 거예요.
이 관계를 알면, 수학 문제를 푸는 데 있어 더 쉽고 빠르게 문제를 풀 수 있을 거예요.
어렵지 않으니 바로 시작해 봅시다.
최대공약수는 영어로 'Greatest Common Factor'입니다. ( 이렇게 떠올리세요! 최대 → 'G'reatest )
그래서 영어의 첫 알파벳을 따서 알파벳 G로,
최소공배수는 영어로 'Least Common Multiple' ( 최소 → 'L'east )이라서 알파벳 L로 흔히 표시합니다.
두 자연수 A, B의 최대공약수를 G, 최소공배수를 L 이라고 하고, 소문자 a, b를 서로소라고 하면 아래와 같이 나타낼 수 있어요

여기서 저랑 같이 볼 부분은 $ A \times B = G \times L $ 이 부분이에요.
$A$ 를 $ G $로 나눈 몫은 $ a $, 이므로 $ A = G \times a $
$B$ 를 $ G $로 나눈 몫은 $ b $, 이므로 $ B = G \times b $
$ A \times B = ( G \times a) \times ( G \times b ) $
여기서 맨 끝의 $ G $ 와 $ b$ 의 자리만 바꾸어주면
$ A \times B = ( G \times a \times b ) \times G $가 됩니다.
( 곱하기에서는 서로 자리를 바꿔도 결과가 똑같이 나온답니다. $ 5 \times 3 =15 $ 과 $ 3 \times 5 =15 $를 계산하면 똑같이 $ 15$ 가 나오는 것처럼요. )
여기서 $ G \times a \times b = L $ 인 최소공배수가 나오므로
$ A \times B = ( G \times a \times b ) \times G = L \times G $ 가 된답니다.
이해를 했으니 한번 12와 18 두 자연수로 예시를 봅시다.
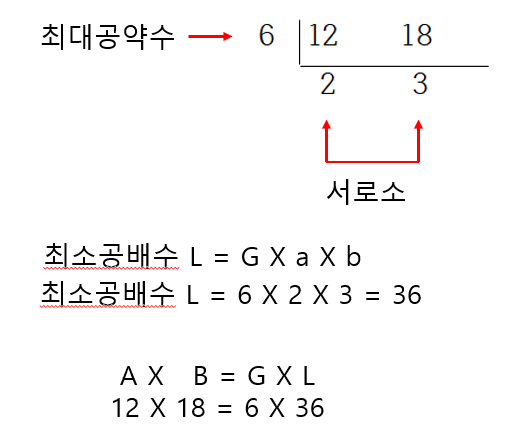
$ 12 \times 18 = 6 \times 36 = 216 $ 으로 똑같이 나오죠?
결론적으로 두 수인 A, B 를 곱했더니 최대공약수와 최소공배수의 곱과 같아졌습니다. 그럼 이 공식이 어디에 유용할까요??
당연히 최대공약수를 구하는 방법과 최소공배수를 구하는 방법의 응용문제를 풀 때 유용하겠죠?
문제를 풀 때 기억해야 할 조건은, 두 수의 곱 또는 최대공약수와 최소공배수의 곱이 문제에 나올 때 이 방법을 떠올리면 된답니다.
( 두 자연수의 곱 ) = ( 최대공약수 ) $ \times $ ( 최소공배수 )
예시 문제를 봅시다.
1. 두 자연수 A, B의 최대공약수가 5이고 최소공배수가 60일 때, $ A \times B $의 값을 구하여라.
문제에서 두 자연수의 곱을 물었으니 당연히 위의 공식을 떠올려야겠죠? 그러면
$ A \times B = 최대공약수 \times 최소공배수 = 5 \times 60 = 300 $ 이 된답니다.
그러므로 정답은 300입니다.
2. 두 자연수의 곱이 108이고 최소공배수가 36일 때, 이 두 자연수의 최대공약수를 구하여라.
두 자연수의 곱이 108이므로 $ A \times B = 108 = 최대공약수 \times 최소공배수 = 최대공약수 \times 36 $ 이므로 최대공약수는 $ 108 \div 36 = 3 $이 됩니다.
그러므로 정답은 $ 3 $ 입니다.
오늘도 공부하느라 고생하셨습니다.
포스팅 상단에 정리 파일이 있습니다.
궁금한 게 있으시다면 댓글에 남겨주시기 바랍니다.
감사합니다.




댓글