정수의 덧셈과 뺄셈의 혼합계산
지금까지 정수와 유리수의 덧셈과 뺄셈을 공부했어요.
오늘은 정수와 유리수의 덧셈과 뺄셈이 같이 있을 때 계산하는 방법을 알아볼 거예요.
계산만 차근차근하면 어렵지 않지만,
부호 실수로 틀리는 경우가 많으니 부호를 잘 확인해서 계산해야 해요.
정수와 유리수의 덧셈과 뺄셈을 잘 모르시는 분은, 아래 링크에서 공부를 하신 후에 이번 시간에 복습하시는 걸 추천해요.
정수와 유리수의 덧셈
정수와 유리수의 덧셈과 연산법칙 ( 중등수학 )
정수와 유리수의 덧셈과 연산법칙 우리가 처음 자연수를 배웠을 때, 가장 먼저 배웠던 게 덧셈과 뺄셈이었을 거예요. 어렸을 때, 기탄 수학 같은 더하기 빼기 연습하는 문제집을 푼 기억이 있나
jwj4519.com
정수와 유리수의 뺄셈
정수와 유리수의 뺄셈 ( 중등 수학 )
정수와 유리수의 뺄셈 저번 시간에 정수와 유리수의 덧셈과 연산법칙에 대해 배웠어요. 더하기를 배웠으니 뺄셈을 배워봐야겠죠?? 저번 시간의 내용을 잘 이해했다면, 별로 어렵지 않으니 걱정
jwj4519.com
자 그럼 바로 시작해볼까요?
정수의 덧셈과 뺄셈의 혼합계산
덧셈과 뺄셈이 같이 있을 때는, 뺄셈을 덧셈으로 고쳐서 계산하는 게 편해요.
예시를 보면서 이해해 봅시다.
참고 : +1, +2, +3,...... 과같은 양수는 1, 2, 3,....... 과같이 +부호를 생략할 수 있어요.
지금부터 계산할 때는, 양수는 부호를 생략해서 나타낼 거예요.
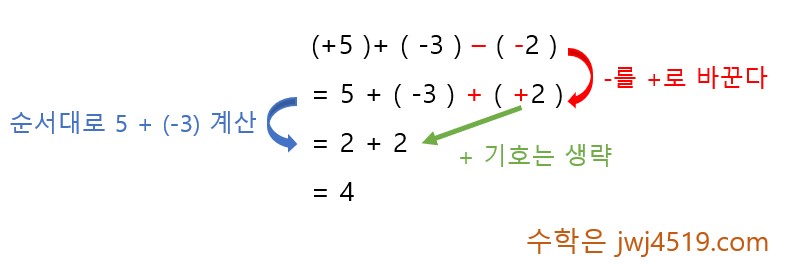
덧셈과 뺄셈이 혼합되어 있는 경우에는 위에서 말했듯이 부호 실수로 정말 많이 틀려요.
그러니 문제를 풀 때, 아래의 순서대로 문제를 풀어보세요.
1. 뺄셈을 덧셈으로 바꾼다.
2. 음수는 항상 괄호를 쳐준다. ( 예 : $-2$가 아니라 $ ( -2 )$ 로 쓴다. )
3. 순서대로 차근차근 계산한다.
위의 3가지만 기억하면, 문제 푸는데 정말 수월할 거예요.
또 다른 예시를 봅시다.

위의 순서대로 위의 예시문제를 풀면 어렵지 않게 이해할 수 있을 거예요.
처음에는 위의 순서를 지키면서 차근차근 앞에꺼부터 계산하다가, 계산이 익숙해지면 아래와 같은 방법으로 문제를 풀어보세요.

첫 번째 풀이 방법과 달라진 점은 딱 1가지예요.
-를 +로 바꾼 다음, 계산이 간단한 $ 4 + (-5) $ 부터 계산해 준거예요.
덧셈에서는 교환법칙이 성립하기 때문에,
$ ( -12 ) + 4 $ 를 먼저 계산하든, $ 4 + (-5)$를 먼저 계산하든,
$ ( -12 ) + 4 + (-5) $ 에서 결과는 똑같이 나와요.
그래서 -를 +로 바꾸는 1번 과정이 끝났으면, 그 뒤부터는 계산이 간단한 것부터 계산하고 차근차근 답을 내주면 된답니다.
예제문제를 보며 한번 잘 이해했나 확인해볼게요.
예제문제 1.
$ ( -6 ) + ( +10 ) - ( -9 ) + ( +4 ) $
( 풀이 )

4 + 9 + 4까지 계산하고 나면, 사람마다 간단한 계산이 달라요.
어떤 사람에게는 4 + 9 + 4 = 13 + 4 = 17 이 편할 수 있고, ( 4 + 9 계산이 편한사람 )
또 다른 사람에게는 4 + 9 + 4 = 8 + 9 =17 이 편할 수도 있어요. ( 4 + 4 계산이 편한사람 )
그러니까 마지막 계산은 자기가 편한 대로 계산하면 된답니다.
자 여기까지 잘 이해했으면, 정수의 덧셈과 뺄셈의 혼합계산에 대해 90% 이상 이해했다고 생각하면 돼요.
정수의 덧셈과 뺄셈의 혼합계산 ( 괄호가 없을 때 )
괄호가 없는 경우의 혼합계산은 빼기만 더하기로 바꾸어주면 돼요.
예시를 봅시다.
$ 6 + 16 - 13 $

괄호가 있을 때랑 별로 다를 게 없죠?
양수는 +를 생략해서 써도 되니까 굳이 6을 (+6)으로 혹은 16을 (+16)으로 쓰지 않아도 된답니다.
정수의 덧셈과 뺄셈 혼합계산 정리
( 1 ) 뺄셈을 덧셈으로 바꾼다.
( 2 ) 음수는 괄호를 쳐준다.
( 3 ) 간단한 계산부터 순서대로 계산한다.
( 4 ) 유리수도 똑같이 계산해준다.
자 그럼 확인문제를 풀어봅시다.
확인문제 1. 다음을 계산하여라.
( 1 ) $ ( -16 ) + ( + 22 ) + ( + 14 ) $
$ ( -16 ) + 22 + 14 $
$ = 6 + 14 $
$ = 20 $
( 2 ) $ -2 + 4 + 6 - 8 $
$ ( -2 ) + 4 + 6 + ( -8 ) $
$ = 2 + 6 + ( - 8 ) $ -2랑 4계산
$ = 8 + ( -8 ) $
$ = 0 $
오늘도 공부하느라 고생하셨습니다.
궁금한 게 있으시면 댓글을 달아주세요.
감사합니다.




댓글