2019 6월 수학나형 29번 짝수형( 고3 대학수학능력시험 6월 모의고사 )

실수 전체의 집합에서 연속이라고 하였으므로,
$a + b = c + \frac52$ 이고
역함수를 갖는다고 하였습니다.
함수 $f(x)$가 역함수 $g(x)$를 갖는다고 하면 두 함수는 $y = x$에서 대칭입니다. 그러므로 $y = f(x)$와 $y = g(x)$의 교점도 $y = x$에 대해 대칭이어야 하므로, 원함수와 역함수의 교점은 $y = x$위이거나 $y = -x + k $위에 존재합니다.
그러고 나서 발문을 보겠습니다. $y = f(x)$와 역함수 $y = f^{-1}(x)$의 그래 표의 교점이 3개이고, 그 교점의 $x$좌표가 각각 $-1, 1, 2$라고 하였습니다. 그러므로 3개의 교점의 $y$좌표가 가질 수 있는 값은 $-1, 1, 2$가 되고 세 점이 $y = x$에 대해서 대칭이 되기 위해서는 $y = f(x)$와 $y = f^{-1}(x)$의 교점은 $(-1, 2), (1, 1), (2, -1)$이 되어야 합니다.
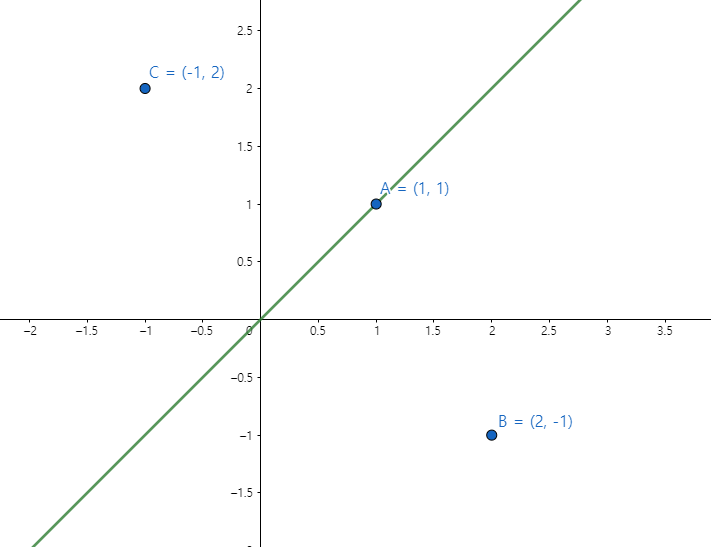
그러므로
$ a + b = c + \frac52 = 1$
$-a + b = 2$
$4c - 5 = -1$
$c = -\frac32$, $a =-\frac12, b = \frac32$가 되어
$2a + 4b - 10c = -1 + 6 +15 = 20$이 정답이 됩니다.
보통 원함수와 역함수의 교점은 $y = x$위에 존재해야 한다고 알고 있는 사람들이 많은데 그 빈틈을 잘 노린 문제였습니다.
감사합니다.




댓글