2020수능 수학가형 29번 짝수형 (대학수학능력시험)

발문에서 주어진 조건을 그림으로 나타내면 아래와 같이 나옵니다.
검은 평면이 $\alpha$가되고, 점 $C$는 평면과 구의 접점이므로 점 $C$와 원점 사이의 거리는 1이 됩니다.

$A(3, -3, 3)$과 $B(-2, 7, -2)$가 주어져 있으므로 점 $O$와의 거리를 구할 수 있습니다. 점 $A, B$의 방향벡터 $U = (5,- 10, 5)$이므로 방향벡터는 $\vec{u} = (1, -2, 1)$이고 점 $A$를 지나므로,
점 $A, B$를 지나는 직선의 방정식은 $\frac{x-3}{1} = \frac{y+3}{-2} = \frac{z-3}{1}$이 됩니다.
이 직선의 방정식 위의 임의의 점은 $T(t+3, -2t-2, t+3)$이므로, AB의 방향벡터 $\vec{u} = (1, -2, 1)$과 $\vec{OT} = (t+3, -2t-2, t+3)$은 수직이므로 내적을 하면 $0$이 나와야 합니다.
$\vec{u} \cdot \vec{OT} = (1, -2, 1) \cdot (t+3, -2t-2, t+3)$ = $(t+3)-2(-2t-2)+(t+3) =0$
$6t +12 = 0$
$t = -2$
그러면 $OT = \sqrt{3}$을 쉽게 구할 수 있으므로 아래와 같이 됩니다.

한편 직선의 방정식$\frac{x-3}{1} = \frac{y+3}{-2} = \frac{z-3}{1}$을 포함하는 모든 평면의 방정식은
$\frac{x-3}{1} = \frac{y+3}{-2}$과 $\frac{x-3}{1} =\frac{z-3}{1}$에서
$-2x + 6 = y+3$과 $x-3 = z-3$
$2x + y -3 = 0$과 $x-z = 0$
$ 2x + y -3 + k(x-z) = 0$으로 표현할 수 있습니다.
정리하면 $ (2+k)x + y - kz -3 = 0$이 됩니다. ( 3차원에서 한직선을 포함하는 평면의 방정식을 구하는 방법은 꼭 기억해 두세요!)
평면 $\alpha, \beta$는 구에 접하므로 원점 $(0, 0, 0)$과의 거리가 1이 나와야 합니다.
$\frac{3}{k^2 + (k+2)^2 +1} = 1$ 정리하면
$k^2 + 2k -2 = 0$
$k = -1 +\sqrt3, -1 - \sqrt3$
$k = -1 + \sqrt3$일때 법선벡터는 $(1 +\sqrt3, 1, 1-\sqrt3)$
$k = -1 - \sqrt3$일때 법선벡터는 $(1-\sqrt3, 1, 1+\sqrt3)$이므로
이면각 $cos(\theta) = \frac{|1-3+1+1-3|}{\sqrt9 + \sqrt9} = \frac13$이 됩니다.
지금까지 조건을 정리해 정사면체를 구하려면 아래와 같이 구하면 됩니다.
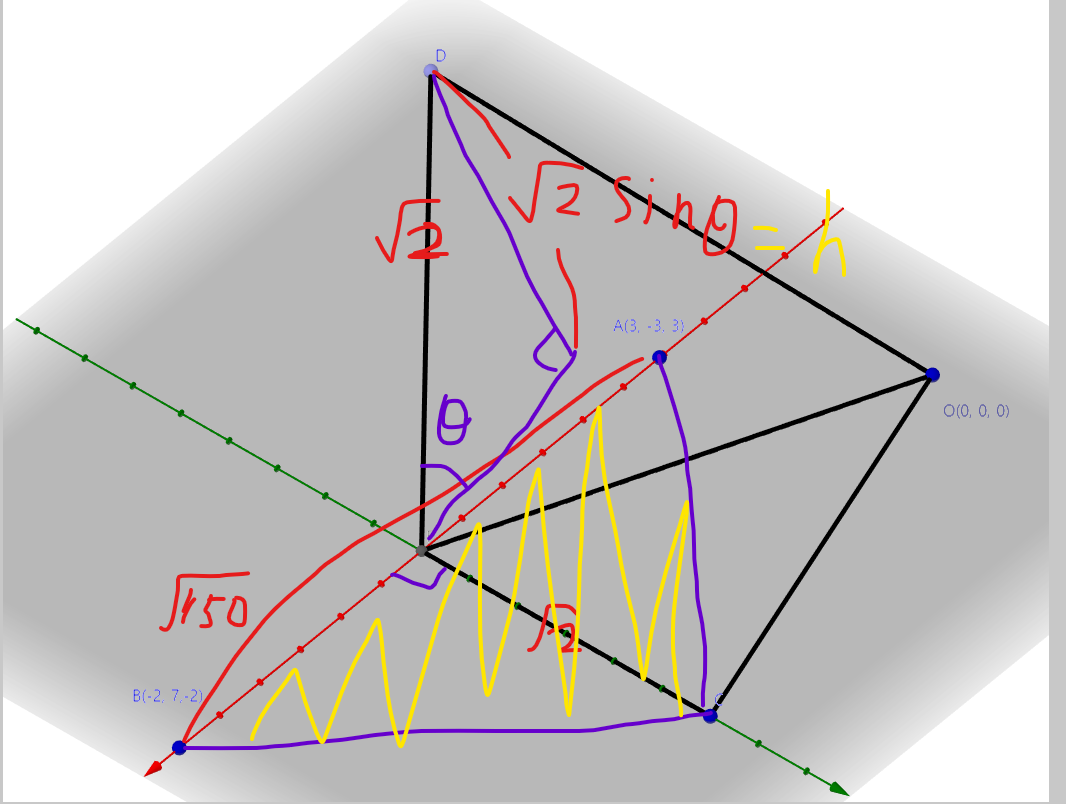
밑면 삼각형 넓이 $S =\sqrt{150} \times \sqrt2 \times \frac12$
높이 $h = \sqrt2 \times \frac{2 \sqrt2}{3}$
$\frac13 \times S \times h = \frac{20}{9} \sqrt3$이 되어 정답은 29가 됩니다.




댓글