2020 6월 수학가형 21번 (고3 대학수학능력시험 6월 모의평가 : 모의고사)

2020_고3_6월모의고사_수학가형.pdf

0.56MB

2020_고3_6월모의고사_수학가형_답지.pdf

0.04MB

안녕하세요. 푸디헬스입니다.

2019년 6월 4일 화요일 한국교육과정평가원의 주관하에 2020 고3 대학수학능력시험 6월 모의평가가 치러졌습니다.

1등급 컷은 89점으로 중상위권 변별이 아주 잘 된 시험이었습니다. 오답률 1위 30번(93%), 오답률 2위 29번(89%), 오답률 3위는 27번(72%)이 차지했습니다. 킬러 문제의 난이도가 줄고 준킬러 문제가 늘어났습니다. 그리고 어느 정도의 정확한 계산을 요구하는 문제도 출제되었습니다. 이번 6평에서의 21번 문제의 오답률은 그리 높지 않지만, 이문제가 계산을 요구하는 문제였고 출제진들이 21번에 배치했다는 것만으로도 의미 있는 문제이니 눈여겨봐야 합니다.

그럼 문제를 풀어보겠습니다.

항상 발문을 읽을 때 한 번에 읽으면 잘 이해가 가지 않거나 헷갈리는 경우가 많습니다. 그래서 발문을 끊어서 읽고 해석하는 게 수학 문제를 푸는데 도움이 됩니다. 여기서 끊어서 읽는 부분은 평가원에서 단어로 제시해줍니다. ~하자라고 정의를 하는 부분까지 끊어 읽고,~일 때처럼 조건을 제시하는 부분까지 끊어 읽으면 문제 해석에 용이합니다.

이것을 수식으로 옮기면 이와 같이 됩니다.

$y = t(x-g(t))+\frac{ln(g(t))}{g(t)}$ 그리고  $x$좌표가 $g(t)$일때 기울기가 $t$라고 하였으므로

$f'(x) = \frac{1-ln(x)}{x^2},  t = \frac{1-ln(g(t))}{g(t)^2}$와같은 식이 나옵니다. 그럼 ~하자라고 정의한 부분까지의 해석이 끝났습니다. 다음 발문으로 가겠습니다.

 

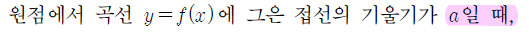
원점에서 곡선 $y = f(x)$에 그은 접선의 기울기가 $a$라고 하였으므로 이때 $y = f(x)$위의 접점의 $x$좌표를 $p = g(a)$라고 하면 이와 같이 됩니다.(기울기가 $t$인 직선이 곡선 $y = f(x)$에 접할 때 접점의 $x$좌표를 $g(t)$라고 하였으므로 $p = g(a)$입니다.) 

이것을 수식으로 나타내면

$y = a(x-p) + f(p)$이고$(0,0)$을 지나므로

$0 = a(0-p) + f(p)$이고 접선의 기울기가 $a$임으로 $f'(p) = \frac{1-ln(p)}{p^2} = a$

$ap = f(p) = \frac{ln(p)}{p} =\frac{1-ln(p)}{p^2} \times p$ 계산하면

$ln(p) = \frac12, p = \sqrt{e} =g(a), a = \frac{1}{2e}$이 됩니다.

 

 

조건의 해석이 끝났음으로 다음 발문으로 가겠습니다.

미분 가능한 함수 $g(t)$에 대해 $a \times g'(a)$를 구하라고 하였습니다. 그러므로 앞에서 구했던 식과 전의 발문에서 구했던 조건을 이용합니다.

$t = \frac{1-ln(g(t))}{g(t)^2}$여기서 $g'(a)$를 구하라고 하였으므로 미분을 합니다.

$t {g(t)^2} = 1-ln(g(t))$ 

$g(t)^2 + 2t g(t) g'(t) = -\frac{g'(t)}{g(t)}$여기서 $t = a$를 대입하면,

$g(a)^2 + 2a g(a) g'(a) = -\frac{g'(a)}{g(a)}$이고 

앞에서 $ln(p) = \frac12, p = \sqrt{e} =g(a), a = \frac{1}{2e}$을 구했으므로 대입하면

$e + 2 \sqrt{e} \times a g'(a)$ = $-\frac{g'(a)}{\sqrt{e}}$ 저희는 $a \times g'(a)$를 구해야 하므로 양변에 $a = \frac{1}{2e}$를 곱합니다.

$\frac{1}{2e} e +\frac{1}{2e} 2 \sqrt{e} \times a g'(a) = - a \frac{g'(a)}{\sqrt{e}}$

$\frac12 +\frac{1}{\sqrt{e}} \times a g'(a) = - \frac{1}{\sqrt{e}} \times a g'(a)$

$a g'(a) = -\frac{\sqrt{e}}{4}$가 됩니다.

발문의 순서대로 문제를 풀면 어렵지 않았습니다. 수험생분들께서 21번을 통해 얻어가실 것은 발문의 순서가 문제 풀이 사고 과정의 순서가 된다는 것입니다.

잘 이해가 가지 않거나 다른 문제의 풀이가 궁금하신 분은 댓글을 남겨주시기 바랍니다. 감사합니다.

 

2020 고3 대학수학능력시험 6월 모의고사 수학 가형 29번, 30번 풀이입니다.

모의고사 - 2020 고3 6월 모의고사 수학 가형 풀이